Page 269 - Dynamics and Control of Nuclear Reactors

APPENDIX D Laplace transforms and transfer functions 271

Example D.2
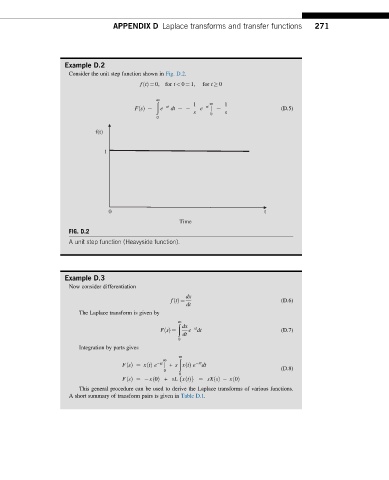
Consider the unit step function shown in Fig. D.2.
ftðÞ ¼ 0, for t < 0 ¼ 1, for t 0

ð ∞ 1 ∞ 1
FsðÞ ¼ e st dt ¼ e st | ¼ (D.5)
s 0 s
0
f(t)

1

0 t
Time
FIG. D.2
A unit step function (Heavyside function).

Example D.3
Now consider differentiation
dx
ftðÞ ¼ (D.6)
dt
The Laplace transform is given by
ð ∞
dx
FsðÞ ¼ e st dt (D.7)
dt
0
Integration by parts gives
ð ∞
∞
FsðÞ ¼ xtðÞ e st | + s xtðÞ e st dt
0 (D.8)
0
f
FsðÞ ¼ x 0ðÞ + sL x tðÞg ¼ sX sðÞ x 0ðÞ
This general procedure can be used to derive the Laplace transforms of various functions.
A short summary of transform pairs is given in Table D.1.