Page 166 - Dynamics of Mechanical Systems

0593_C05_fm Page 147 Monday, May 6, 2002 2:15 PM

Planar Motion of Rigid Bodies — Methods of Analysis 147

5.7 Instant Center, Analytical Considerations
In Section 5.4, we developed an intuitive and geometrical description of centers of zero
velocity. Here, we examine these concepts again, but this time from a more analytical
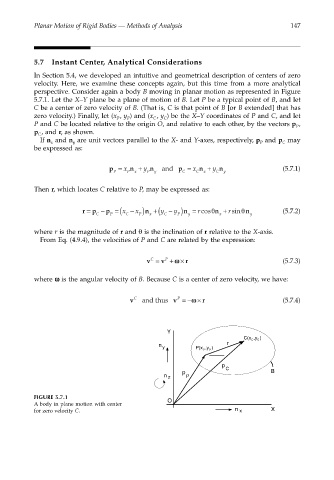
perspective. Consider again a body B moving in planar motion as represented in Figure
5.7.1. Let the X–Y plane be a plane of motion of B. Let P be a typical point of B, and let
C be a center of zero velocity of B. (That is, C is that point of B [or B extended] that has
zero velocity.) Finally, let (x , y ) and (x , y ) be the X–Y coordinates of P and C, and let
P P C C
P and C be located relative to the origin O, and relative to each other, by the vectors p ,
P
p , and r, as shown.
C
If n and n are unit vectors parallel to the X- and Y-axes, respectively, p and p may
x y P C
be expressed as:
p = x n + y n and p = x n + y n (5.7.1)
P P x P y C C x C y

Then r, which locates C relative to P, may be expressed as:

r = p − x − x n ) y − y n ) = rcosθ n + rsinθ n (5.7.2)
C p = ( C P x +( C P y x y
P
where r is the magnitude of r and θ is the inclination of r relative to the X-axis.
From Eq. (4.9.4), the velocities of P and C are related by the expression:

v = v + ωω × r (5.7.3)
P
C
where ωω ωω is the angular velocity of B. Because C is a center of zero velocity, we have:

ω
ω
P
C
v and thus v =− × r (5.7.4)
Y
C(x ,y )
C
C
n r
y P(x ,y )
P P

p
C
p B
n z P
FIGURE 5.7.1
A body in plane motion with center O
for zero velocity C. n x X