Page 183 - Dynamics of Mechanical Systems

0593_C06_fm Page 164 Monday, May 6, 2002 2:28 PM

164 Dynamics of Mechanical Systems

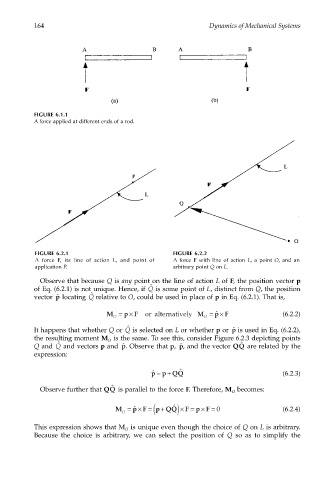
FIGURE 6.1.1
A force applied at different ends of a rod.

FIGURE 6.2.1 FIGURE 6.2.2
A force F, its line of action L, and point of A force F with line of action L, a point O, and an
application P. arbitrary point Q on L.
Observe that because Q is any point on the line of action L of F, the position vector p
ˆ
of Eq. (6.2.1) is not unique. Hence, if is some point of L, distinct from Q, the position
Q
ˆ
ˆ p
Q
vector locating relative to O, could be used in place of p in Eq. (6.2.1). That is,
×
M = p F or alternatively M = ˆ × (6.2.2)
p F
O
O
ˆ
It happens that whether Q or is selected on L or whether p or is used in Eq. (6.2.2),
ˆ p
Q
the resulting moment M is the same. To see this, consider Figure 6.2.3 depicting points
O
ˆ
ˆ
Q and and vectors p and . Observe that p, , and the vector Q are related by the
Q
Q
ˆ p
ˆ p
expression:
ˆ p = p QQ (6.2.3)
ˆ
+
ˆ
Observe further that Q is parallel to the force F. Therefore, M becomes:
Q
O
)
+
×
ˆ
M = ˆ p F = ( p QQ ×= p F×= 0 (6.2.4)
F
O
This expression shows that M is unique even though the choice of Q on L is arbitrary.
O
Because the choice is arbitrary, we can select the position of Q so as to simplify the