Page 334 - Electrical Properties of Materials

316 Lasers

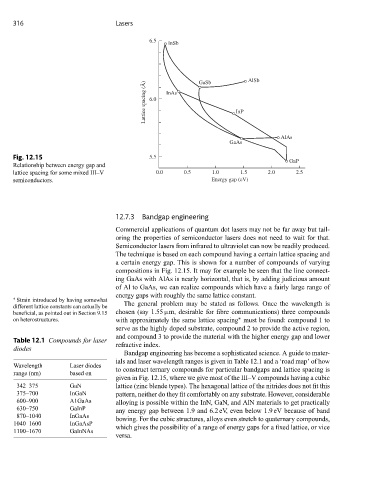
6.5
InSb

AlSb
GaSb
Lattice spacing (Å) 6.0 InAs InP

AlAs
GaAs

Fig. 12.15 5.5
GaP
Relationship between energy gap and
lattice spacing for some mixed III–V 0.0 0.5 1.0 1.5 2.0 2.5
semiconductors. Energy gap (eV)

12.7.3 Bandgap engineering
Commercial applications of quantum dot lasers may not be far away but tail-
oring the properties of semiconductor lasers does not need to wait for that.
Semiconductor lasers from infrared to ultraviolet can now be readily produced.
The technique is based on each compound having a certain lattice spacing and
a certain energy gap. This is shown for a number of compounds of varying
compositions in Fig. 12.15. It may for example be seen that the line connect-
ing GaAs with AlAs is nearly horizontal, that is, by adding judicious amount
of Al to GaAs, we can realize compounds which have a fairly large range of
energy gaps with roughly the same lattice constant.
∗ Strain introduced by having somewhat
different lattice constants can actually be The general problem may be stated as follows. Once the wavelength is
beneficial, as pointed out in Section 9.15 chosen (say 1.55 μm, desirable for fibre communications) three compounds
∗
on heterostructures. with approximately the same lattice spacing must be found: compound 1 to
serve as the highly doped substrate, compound 2 to provide the active region,
and compound 3 to provide the material with the higher energy gap and lower
Table 12.1 Compounds for laser
refractive index.
diodes
Bandgap engineering has become a sophisticated science. A guide to mater-
ials and laser wavelength ranges is given in Table 12.1 and a ‘road map’ of how
Wavelength Laser diodes
to construct ternary compounds for particular bandgaps and lattice spacing is
range (nm) based on
given in Fig. 12.15, where we give most of the III–V compounds having a cubic
342–375 GaN lattice (zinc blende types). The hexagonal lattice of the nitrides does not fit this
375–700 InGaN pattern, neither do they fit comfortably on any substrate. However, considerable
600–900 A1GaAs alloying is possible within the InN, GaN, and AlN materials to get practically
630–750 GaInP
any energy gap between 1.9 and 6.2 eV, even below 1.9 eV because of band
870–1040 InGaAs
bowing. For the cubic structures, alloys even stretch to quaternary compounds,
1040–1600 InGaAsP
which gives the possibility of a range of energy gaps for a fixed lattice, or vice
1100–1670 GaInNAs
versa.