Page 391 - Electrical Properties of Materials

The effect of a magnetic field 373

(a) (b)

a
Energy Energy b

0 Momentum 0 Momentum
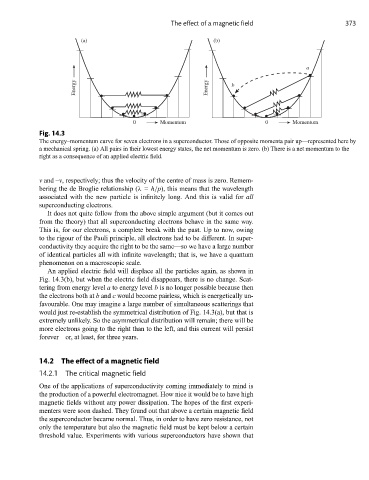
Fig. 14.3
The energy–momentum curve for seven electrons in a superconductor. Those of opposite momenta pair up—represented here by
a mechanical spring. (a) All pairs in their lowest energy states, the net momentum is zero. (b) There is a net momentum to the
right as a consequence of an applied electric field.

v and –v, respectively; thus the velocity of the centre of mass is zero. Remem-
bering the de Broglie relationship (λ = h/p), this means that the wavelength
associated with the new particle is infinitely long. And this is valid for all
superconducting electrons.
It does not quite follow from the above simple argument (but it comes out
from the theory) that all superconducting electrons behave in the same way.
This is, for our electrons, a complete break with the past. Up to now, owing
to the rigour of the Pauli principle, all electrons had to be different. In super-
conductivity they acquire the right to be the same—so we have a large number
of identical particles all with infinite wavelength; that is, we have a quantum
phenomenon on a macroscopic scale.
An applied electric field will displace all the particles again, as shown in
Fig. 14.3(b), but when the electric field disappears, there is no change. Scat-
tering from energy level a to energy level b is no longer possible because then
the electrons both at b and c would become pairless, which is energetically un-
favourable. One may imagine a large number of simultaneous scatterings that
would just re-establish the symmetrical distribution of Fig. 14.3(a), but that is
extremely unlikely. So the asymmetrical distribution will remain; there will be
more electrons going to the right than to the left, and this current will persist
forever—or, at least, for three years.

14.2 The effect of a magnetic field
14.2.1 The critical magnetic field

One of the applications of superconductivity coming immediately to mind is
the production of a powerful electromagnet. How nice it would be to have high
magnetic fields without any power dissipation. The hopes of the first experi-
menters were soon dashed. They found out that above a certain magnetic field
the superconductor became normal. Thus, in order to have zero resistance, not
only the temperature but also the magnetic field must be kept below a certain
threshold value. Experiments with various superconductors have shown that