Page 390 - Electrical Properties of Materials

372 Superconductivity

(a) (b)

a
Energy Energy b

I 0 Momentum 0 Momentum
0
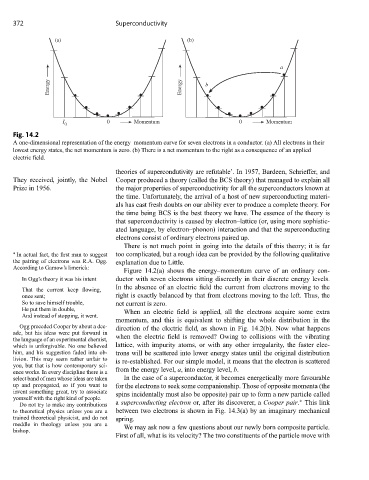
Fig. 14.2
A one-dimensional representation of the energy–momentum curve for seven electrons in a conductor. (a) All electrons in their
lowest energy states, the net momentum is zero. (b) There is a net momentum to the right as a consequence of an applied
electric field.

theories of supercondutivity are refutable’. In 1957, Bardeen, Schrieffer, and
They received, jointly, the Nobel Cooper produced a theory (called the BCS theory) that managed to explain all
Prize in 1956. the major properties of superconductivity for all the superconductors known at
the time. Unfortunately, the arrival of a host of new superconducting materi-
als has cast fresh doubts on our ability ever to produce a complete theory. For
the time being BCS is the best theory we have. The essence of the theory is
that superconductivity is caused by electron–lattice (or, using more sophistic-
ated language, by electron–phonon) interaction and that the superconducting
electrons consist of ordinary electrons paired up.
There is not much point in going into the details of this theory; it is far
∗ In actual fact, the first man to suggest too complicated, but a rough idea can be provided by the following qualitative
the pairing of electrons was R.A. Ogg. explanation due to Little.
According to Gamow’s limerick:
Figure 14.2(a) shows the energy–momentum curve of an ordinary con-
In Ogg’s theory it was his intent ductor with seven electrons sitting discreetly in their discrete energy levels.
In the absence of an electric field the current from electrons moving to the
That the current keep flowing,
once sent; right is exactly balanced by that from electrons moving to the left. Thus, the
So to save himself trouble, net current is zero.
He put them in double, When an electric field is applied, all the electrons acquire some extra
And instead of stopping, it went.
momentum, and this is equivalent to shifting the whole distribution in the
Ogg preceded Cooper by about a dec- direction of the electric field, as shown in Fig. 14.2(b). Now what happens
ade, but his ideas were put forward in
the language of an experimental chemist, when the electric field is removed? Owing to collisions with the vibrating
which is unforgivable. No one believed lattice, with impurity atoms, or with any other irregularity, the faster elec-
him, and his suggestion faded into ob- trons will be scattered into lower energy states until the original distribution
livion. This may seem rather unfair to is re-established. For our simple model, it means that the electron is scattered
you, but that is how contemporary sci-
ence works. In every discipline there is a from the energy level, a, into energy level, b.
select band of men whose ideas are taken In the case of a superconductor, it becomes energetically more favourable
up and propagated, so if you want to for the electrons to seek some companionship. Those of opposite momenta (the
invent something great, try to associate spins incidentally must also be opposite) pair up to form a new particle called
yourself with the right kind of people. ∗
Do not try to make any contributions a superconducting electron or, after its discoverer, a Cooper pair. This link
to theoretical physics unless you are a between two electrons is shown in Fig. 14.3(a) by an imaginary mechanical
trained theoretical physicist, and do not spring.
meddle in theology unless you are a We may ask now a few questions about our newly born composite particle.
bishop.
First of all, what is its velocity? The two constituents of the particle move with