Page 176 - Elements of Chemical Reaction Engineering 3rd Edition

1 48 Isothermal Reactor Design Chap. 4

Reactor volume
for a second-order
gas-phase reaction

If we &vide both sides of Equation (4-17) by the cross-sectional area of
the reactor, A,, we obtain the following equation relating reactor length to con-
version:

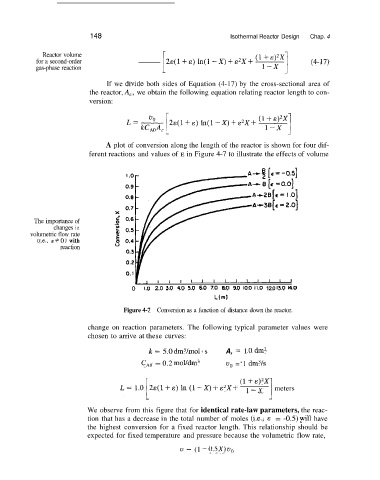
A plot of conversion along the length of the reactor is shown for four dif-
ferent reactions and values of E in Figure 4-7 to illustrate the effects of volume

The importance of
changes in
volumetric flow rate
(i.e., E ;ti 0 ) with
reaction

L.1 I I I f ’ 1 1 ” ’ ” ’
o 1.0 2.0 3.0 4.0 5.0 6.0 7.0 a0 90 10.0 11.0 12.0 13.0 14.0
L(m)
Figure 4-7 Conversion as a function of distance down the reactor.

change on reaction parameters. The following typical parameter values were
chosen to arrive at these curves:

k = 5.0 dm3/11101* s A, = 1 .O dm2
C,, = 0.2 moUdm3 u0 =‘1 dm3/s
1
(1 + &)2X
2~(1+c)ln(l-X)+~~X+ 1-x meters

We observe from this figure that for identical rate-law parameters, the reac-
tion that has a decrease in the total number of moles (i.e., c = -0.5) pill have
the highest conversion for a fixed reactor length. This relationship should be
expected for fixed temperature and pressure because the volumetric flow rate,
u = (1 -0.5X)~~