Page 415 - Academic Press Encyclopedia of Physical Science and Technology 3rd Analytical Chemistry

P1: GLQ Final pages
Encyclopedia of Physical Science and Technology EN012C-568 July 26, 2001 15:32

Photoelectron Spectroscopy 65

experiment to a plot of “depth versus composition,” it is states. The resulting electrons are ejected from the ex-
necessary to deconvolute the observed data. A number of citation region and measured. This combination of laser
algorithms for such a deconvolution has been published excitation and pulsed-field ionization makes it possible to
but as the experimental data always contain some amount resolve the rotational structure of small molecular ions
of statistical error, it is often more appropriate to compare and the vibrational structure of larger ones.
curves obtained for certain layer models with the experi-
mental data.
II. PHOTOEMISSION FROM ATOMS,
MOLECULES, AND SOLIDS
H. Spin-Resolved Photoelectron Spectra
In spin-resolved photoelectron spectroscopy (SRPES), A. The Independent-Particle Model
one makes use of the fact that a single electron has a spin.
To elucidate the information obtainable by PES, we start
In a properly designed instrument, the orientation of the
with the independent-particle model. This model is best
spin with respect to the laboratory frame does not change
known for atoms. The electronic structure of an atom is
from the moment the electron leaves the sample to the
described by orbitals ϕ(q i ), which are functions of the
moment it hits the detector, or if it changes, it changes in
spatial coordinates q i . Each orbital can hold a maximum
a well-defined manner. If the detector is sensitive to the
of two electrons if these electrons have antiparallel spin.
orientation of the spin, as for example, a Mott-detector
With each orbital we can associate an orbital energy ε i .
(see Section III.E), information is obtained on the spin
According to the aufbau principle, the state of lowest total
distribution of the photoelectrons that leave the sample.
energy is reached if the orbitals are filled in the order of
For a nonmagnetic sample, the spin distribution is usu-
increasing orbital energy. Some of the orbitals are degen-
ally random, and no additional information is gained. For
erate with respect to orbital energy, and Hund’s rule states
a magnetic sample, however, the ratio of the number of
that degenerate orbitals are first filled singly with electrons
electrons that are emitted with spin-up to the number of
of parallel spin. The orbitals holding the inner shell or core
electrons with spin-down depends on the band structure
electrons are energetically well separated from the orbitals
of the system and therefore on the binding energy. The
of the outermost or “valence” electrons (Table III). For
combination of spin-resolved and angular-resolved PES
most atoms the valence electrons have binding energies
has contributed tremendously to the understanding of all
of less than 40 eV. If the state of lowest energy consists
kinds of magnetic materials.
only of doubly occupied orbitals, it is called a “closed
shell ground state.” This situation is depicted in Fig. 8a.
I. Zero Kinetic Energy Photoelectron Spectra The rest of this article will be restricted to the discussion
Over the last years zero kinetic energy (ZEKE) spec-
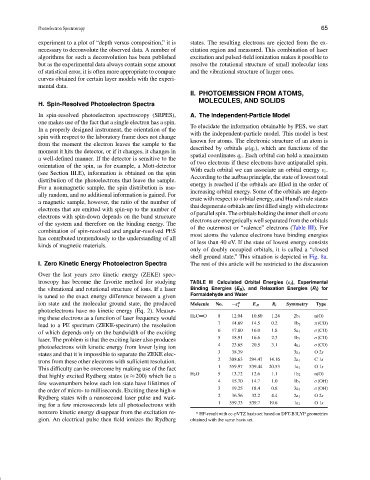
troscopy has become the favorite method for studying TABLE III Calculated Orbital Energies (ε i ), Experimental
the vibrational and rotational structure of ions. If a laser Binding Energies (E B ), and Relaxation Energies (R i )for
is tuned to the exact energy difference between a given Formaldehyde and Water
ion state and the molecular ground state, the produced Molecule No. −ε a E B R i Symmetry Type
i
photoelectrons have no kinetic energy (Eq. 2). Measur-
ing these electrons as a function of laser frequency would H 2 C O 8 12.04 10.80 1.24 2b 1 n(O)
lead to a PE spectrum (ZEKE-spectrum) the resolution 7 14.69 14.5 0.2 1b 2 π(CO)
of which depends only on the bandwidth of the exciting 6 17.80 16.0 1.8 5a 1 σ(CH)
laser. The problem is that the exciting laser also produces 5 18.91 16.6 2.3 1b 1 σ(CH)
photoelectrons with kinetic energy from lower lying ion 4 23.65 20.5 3.1 4a 1 σ(CO)
3 38.39 3a 1 O2s
states and that it is impossible to separate the ZEKE elec-
2 308.63 294.47 14.16 2a 1 C1s
trons from these other electrons with sufficient resolution.
1 559.97 539.44 20.53 O1s
This difficulty can be overcome by making use of the fact 1a 1
that highly excited Rydberg states (n ≈ 200) which lie a H 2 O 5 13.72 12.6 1.1 1b 2 n(O)
few wavenumbers below each ion state have lifetimes of 4 15.70 14.7 1.0 1b 1 σ(OH)
the order of micro- to milliseconds. Exciting these high-n 3 19.25 18.4 0.8 3a 1 σ(OH)
Rydberg states with a nanosecond laser pulse and wait- 2 36.56 32.2 4.4 2a 1 O2s
ing for a few microseconds lets all photoelectrons with 1 559.33 539.7 19.6 1a 1 O1s
nonzero kinetic energy disappear from the excitation re- a HF-result with cc-pVTZ basis set based on DFT-B3LYP geometries
gion. An electrical pulse then field ionizes the Rydberg obtained with the same basis set.