Page 413 - Academic Press Encyclopedia of Physical Science and Technology 3rd Analytical Chemistry

P1: GLQ Final pages
Encyclopedia of Physical Science and Technology EN012C-568 July 26, 2001 15:32

Photoelectron Spectroscopy 63

F. Angular Distribution of Photoelectrons For unpolarized exciting radiation, the emission is
isotropic around the incident beam. In this case the an-
For a single atom or molecule, the probability of emission
gular distribution depends only on the angle θ between
of an electron into a certain direction with respect to an
the propagation direction of the radiation and the direc-
internal coordinate system is not isotropic. It depends on
tion of the outgoing electron. We obtain
the initial and final states of the photoemission process,
2
the orientation of the electric vector E of the ionizing ra- I(θ) = (σ/4π)[1 + (β/2)(3/2 sin θ − 1)] (6)
diation, and the energy hν. For example, if the electron
It is possible to measure σ and β even with unpolarized
is removed from an s orbital of an atom, the probability
radiation. If the emitted photoelectrons are observed un-
of finding the outgoing electron under an angle φ with re- der an angle of θ = 54 44 (the “magic angle”), the term

◦
2
spect to E is proportional to cos φ. Thus, the probability 2
(3/2 sin θ − 1) vanishes and the isotropic cross section σ
distribution looks like an atomic p orbital.
is obtained directly. This “magic angle” is used in most
In a gaseous sample the molecules are randomly ori-
commercially available PE spectrometers, also in those
ented with respect to a laboratory fixed coordinate system.
which are designed for the investigation of solid samples.
To derive the angular distribution I(φ) in the laboratory
system, we must integrate over all possible orientations of
the molecules. If the ionizing radiation is linearly polar- G. Angle-Resolved Photoelectron Spectra
ized, I(φ) can be expressed as
A different situation occurs if a molecule is adsorbed at
2
I(φ) = (σ/4π)[1 + (β/2)(3 cos φ − 1)] (5) a surface and thereby fixed in space. For example, con-
sider a rodlike molecule (e.g., CO) which, for a given final
where σ is the isotropic cross section and β the “asym- +
state M , emits electrons preferentially in the direction of
i
metry parameter.” The possible range of β is −1to +2.
the molecular axis. In addition, assume that the emission
Both σ and β depend on the initial and final states of the 2
probability is proportional to cos of the angle between
photoemission process as well as the kinetic energy of
molecular axis and electric vector E of the ionizing radia-
the outgoing electron, with σ often showing strong vari-
tion. The system is fully described by three angles and the
ations at low kinetic energies and a smooth decrease at
polarization of the radiation. The three angles are shown
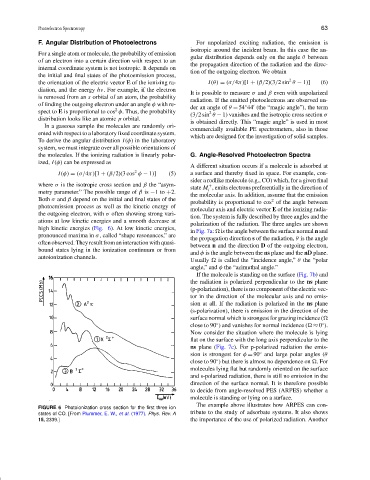
high kinetic energies (Fig. 6). At low kinetic energies,
in Fig. 7a:
is the angle between the surface normal n and
pronounced maxima in σ, called “shape resonances,” are
the propagation direction s of the radiation, θ is the angle
often observed. They result from an interaction with quasi- between n and the direction D of the outgoing electron,
bound states lying in the ionization continuum or from
and φ is the angle between the ns plane and the nD plane.
autoionization channels.
Usually
is called the “incidence angle,” θ the “polar
angle,” and φ the “azimuthal angle.”
If the molecule is standing on the surface (Fig. 7b) and
the radiation is polarized perpendicular to the ns plane
(p-polarization), there is no component of the electric vec-
tor in the direction of the molecular axis and no emis-
sion at all. If the radiation is polarized in the ns plane
(s-polarization), there is emission in the direction of the
surface normal which is strongest for grazing incidence (
◦
close to 90 ) and vanishes for normal incidence (
≈ 0 ).
◦
Now consider the situation where the molecule is lying
flat on the surface with the long axis perpendicular to the
ns plane (Fig. 7c). For p-polarized radiation the emis-
sion is strongest for φ = 90 and large polar angles (θ
◦
close to 90 ) but there is almost no dependence on
.For
◦
molecules lying flat but randomly oriented on the surface
and s-polarized radiation, there is still no emission in the
direction of the surface normal. It is therefore possible
to decide from angle-resolved PES (ARPES) whether a
molecule is standing or lying on a surface.
The example above illustrates how ARPES can con-
FIGURE 6 Photoionization cross section for the first three ion
states of CO. [From Plummer, E. W., et al. (1977). Phys. Rev. A tribute to the study of adsorbate systems. It also shows
15, 2339.] the importance of the use of polarized radiation. Another