Page 432 - Academic Press Encyclopedia of Physical Science and Technology 3rd Analytical Chemistry

P1: GLQ Final pages
Encyclopedia of Physical Science and Technology EN012C-568 July 26, 2001 15:32

82 Photoelectron Spectroscopy

B. Energy Band Mapping
The quadratic relation between energy and momentum
that holds for a free electron is no longer valid in a crys-
talline solid, where the electron moves under the influence
of the periodic lattice potential. The relation between elec-
tron energy and electron momentum along certain direc-
tions within the Brillouin zone is called the “band struc-
ture”ofthesolid.Angle-resolvedPESispresentlytheonly
method that allows an experimental determination of the
band dispersion (the relation between energy and momen-
tum) of occupied bands that do not lie close to the Fermi
energy. This capability is due to the fact that the photon
adds only negligibly to the electron momentum. Because
of momentum conservation, the momentum of the created
photoelectron (p PE ) is the same as that of the electron in
the initial state band (p i ). The simultaneous fulfillment of
energy conservation

E kin = hν − E B (20)
and momentum conservation

p PE = p i (21)
has consequences that can be understood from the simpli-
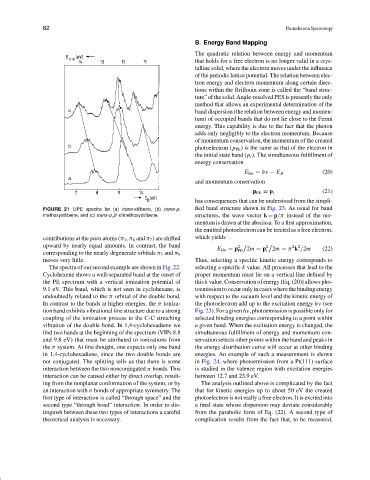
FIGURE 21 UPE spectra for (a) trans-stilbene, (b) trans-p- fied band structure shown in Fig. 23. As usual for band
methoxystilbene, and (c) trans-p,p -dimethoxystilbene. structures, the wave vector k = p/π instead of the mo-

mentum is drawn at the abscissa. To a first approximation,
the emitted photoelectron can be treated as a free electron,
contributions at the para atoms (π 3 , π 4 and π 7 ) are shifted which yields
upward by nearly equal amounts. In contrast, the band 2 2 2 2
E kin = p 2m = p 2m = π k /2m (22)
PE i
corresponding to the nearly degenerate orbitals π 5 and π 6
moves very little. Thus, selecting a specific kinetic energy corresponds to
The spectra of our second example are shown in Fig. 22. selecting a specific k value. All processes that lead to the
Cyclohexene shows a well-separated band at the onset of proper momentum must lie on a vertical line defined by
the PE spectrum with a vertical ionization potential of this k value. Conservation of energy [Eq. (20)] allows pho-
9.1 eV. This band, which is not seen in cyclohexane, is toemission to occur only in cases where the binding energy
undoubtedly related to the π orbital of the double bond. with respect to the vacuum level and the kinetic energy of
In contrast to the bands at higher energies, the π ioniza- the photoelectron add up to the excitation energy hν (see
tion band exhibits vibrational fine structure due to a strong Fig. 23). For a given h ν, photoemission is possible only for
coupling of the ionization process to the C-C stretching selected binding energies corresponding to a point within
vibration of the double bond. In 1,4-cyclohexadiene we a given band. When the excitation energy is changed, the
find two bands at the beginning of the spectrum (VIPs 8.8 simultaneous fulfillment of energy and momentum con-
and 9.8 eV) that must be attributed to ionizations from servation selects other points within the band and peaks in
the π system. At first thought, one expects only one band the energy distribution curve will occur at other binding
in 1,4-cyclohexadiene, since the two double bonds are energies. An example of such a measurement is shown
not conjugated. The splitting tells us that there is some in Fig. 24, where photoemission from a Pt(111) surface
interaction between the two nonconjugated π bonds. This is studied in the valence region with excitation energies
interaction can be caused either by direct overlap, result- between 12.7 and 23.9 eV.
ing from the nonplanar conformation of the system, or by The analysis outlined above is complicated by the fact
an interaction with σ bonds of appropriate symmetry. The that for kinetic energies up to about 50 eV the created
first type of interaction is called “through space” and the photoelectron is not really a free electron. It is excited into
second type “through bond” interaction. In order to dis- a final state whose dispersion may deviate considerably
tinguish between these two types of interactions a careful from the parabolic form of Eq. (22). A second type of
theoretical analysis is necessary. complication results from the fact that, to be measured,