Page 282 - Engineered Interfaces in Fiber Reinforced Composites

Chapter 6. Interface mechanics and fracture toughness theories 263

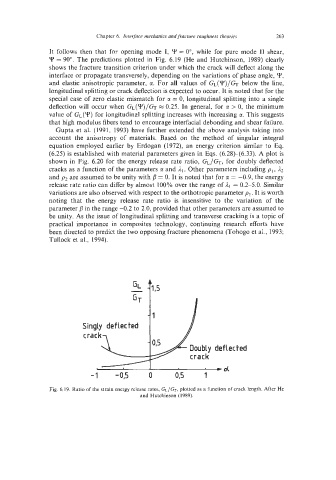
It follows then that for opening mode I, Y = O", while for pure mode I1 shear,
Y = 90". The predictions plotted in Fig. 6.19 (He and Hutchinson, 1989) clearly
shows the fracture transition criterion under which the crack will deflect along the
interface or propagate transversely, depending on the variations of phase angle, Y,
and elastic anisotropic parameter, a. For all values of GL('€')/& below the line,
longitudinal splitting or crack deflection is expected to occur. It is noted that for the
special case of zero elastic mismatch for a = 0, longitudinal splitting into a single
deflection will occur when GL(Y)/GT x 0.25. In general, for CI > 0, the minimum
value of GL(") for longitudinal splitting increases with increasing a. This suggests
that high modulus fibers tend to encourage interfacial debonding and shear failure.
Gupta et al. (1991, 1993) have further extended the above analysis taking into
account the anisotropy of materials. Based on the method of singular integral
equation employed earlier by Erdogan (1972), an energy criterion similar to Eq.
(6.25) is established with material parameters given in Eqs. (6.28)-(6.33). A plot is
shown in Fig. 6.20 for the energy release rate ratio, GL/GT, for doubly deflected
cracks as a function of the parameters a and 11. Other parameters including pi, 22
and p2 are assumed to be unity with p = 0. It is noted that for a = -0.9, the energy
release rate ratio can differ by almost 100% over the range of ill = 0.2-5.0. Similar
variations are also observed with respect to the orthotropic parameter p, . It is worth
noting that the energy release rate ratio is insensitive to the variation of the
parameter p in the range -0.2 to 2.0, provided that other parameters are assumed to
be unity. As the issue of longitudinal splitting and transverse cracking is a topic of
practical importance in composites technology, continuing research efforts have
been directed to predict the two opposing fracture phenomena (Tohogo et al., 1993;
Tullock et al., 1994).

Singly deflected

-d
-1 - 0,s 0 015 1

Fig. 6.19. Ratio of the strain energy release rates, GL/GT, plotted as a function of crack length. After He
and Hutchinson (1989).