Page 262 - Environmental Nanotechnology Applications and Impacts of Nanomaterials

Nanoparticle Transport, Aggregation, and Deposition 247

as they approach one another. If we describe aggregation as occurring
between two groups of identically sized particles, each with an initial
concentration equal to one-half of the total number concentration n , the
j
solution to equation 12 for the time t required to reduce the initial
a
particle concentration to a fraction (1 – n /n ) of its initial value through
j
j0
aggregation is:
n
4 j0
t c 5 a 2 1b (13)
ab n n j
jj j0
From Eq. 13 it becomes evident that t a varies inversely with the colli-
sion frequency ij and with the initial particle concentration n j0 .
In a simple system where particle collisions occur via the rectilinear
model as a result of Brownian motion and mechanical stirring in the sus-
pension (thus ignoring settling, which should be minimal for nanopar-
ticles), then jj jj Br + jjsh can be expressed from Eqs. 9 and 10 as:

8kT 32 3
b 5 1 r G m (14)
j
3m 3
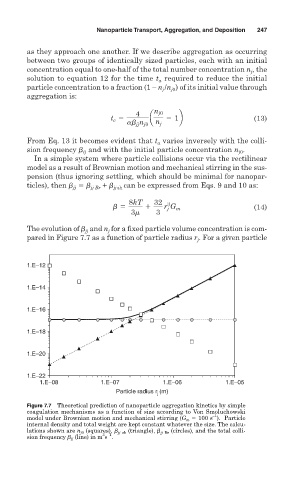
The evolution of and n for a fixed particle volume concentration is com-
j
jj
pared in Figure 7.7 as a function of particle radius r . For a given particle
j
1.E–12

1.E–14

1.E–16

1.E–18

1.E–20

1.E–22
1.E–08 1.E–07 1.E–06 1.E–05
Particle radius r (m)
j
Figure 7.7 Theoretical prediction of nanoparticle aggregation kinetics by simple
coagulation mechanisms as a function of size according to Von Smoluchowski
–1
model under Brownian motion and mechanical stirring (G m 100 s ). Particle
internal density and total weight are kept constant whatever the size. The calcu-
lations shown are n j0 (squares), jj sh (triangle), jj Br (circles), and the total colli-
3 –1
sion frequency jj (line) in m s .