Page 111 - Essentials of physical chemistry

The First Law of Thermodynamics 73

TEMPERATURE DEPENDENCE OF REACTION ENTHALPIES

0
Do all reactions occur at 258C? Of course not! Thus, we need a way to use H values for reactions at
f

qH
, that is, C P is the amount
qT
other temperatures. The hint of an approach is to note that C P ¼
P
by which H changes with temperature at constant pressure. In fact we can integrate C P over a range
0
of temperatures to correct H for temperatures other than 298.158K.
f
ð T ð T ð T
qH
dH ¼ H T H 298:15 :
C P dT ¼ dt ¼
qT P
298:15 298:15 298:15
T
ð
C P dT. However, C P may depend on the temperature such as C P (T).
Thus, H T ¼ H 298:15 þ
298:15
ð T
0
H ¼ H 0 C P (T)dT:
T 298:15 þ
298:15
Since we may want to use a C P value not at one of the tabulated temperatures we can fita
polynomial to discrete values of C P in terms of T. Here ‘‘e’’ is simply the fifth numerical coefficient.
3
2
C P ffi a þ bT þ cT þ dT þ eT 4
3
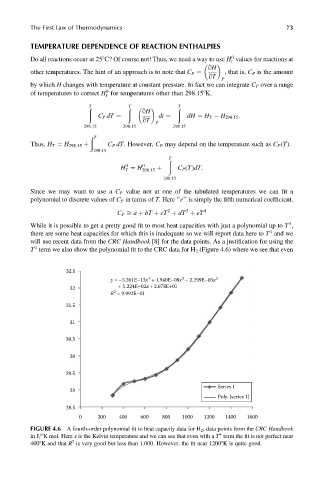
While it is possible to get a pretty good fit to most heat capacities with just a polynomial up to T ,
4
there are some heat capacities for which this is inadequate so we will report data here to T and we
will use recent data from the CRC Handbook [8] for the data points. As a justification for using the
4
T term we also show the polynomial fit to the CRC data for H 2 (Figure 4.6) where we see that even
32.5
y = –5.261E–12x + 1.940E–08x – 2.299E–05x 2
4
3
+ 1.224E–02x + 2.678E+01
32
2
R = 9.992E–01
31.5
31

30.5

30

29.5

Series 1
29
Poly. (series 1)
28.5
0 200 400 600 800 1000 1200 1400 1600
FIGURE 4.6 A fourth-order polynomial fit to heat capacity data for H 2 ; data points from the CRC Handbook
4
in J=8K mol. Here x is the Kelvin temperature and we can see that even with a T term the fit is not perfect near
2
4008K and that R is very good but less than 1.000. However, the fit near 12008K is quite good.