Page 278 - Essentials of physical chemistry

240 Essentials of Physical Chemistry

TABLE 11.2
Molecular Orbitals for trans-Butadiene,
2Pz Coefficients by Column
* *
p 1 p 2 p 3 p 4
2Pz(1) 0.376 0.525 0.618 0.502
2Pz(2) 0.488 0.403 0.462 0.682
2Pz(3) 0.488 0.403 0.462 0.682
2Pz(4) 0.376 0.525 0.618 0.502
Note: Weighting coefficients of an STO-3G SCF-MO
calculation, see Chapter 17.

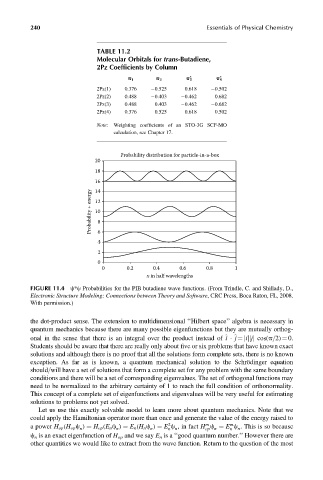
Probability distribution for particle-in-a-box
20
18
16
Probability + energy 12 8
14

10

4 6
2
0
0 0.2 0.4 0.6 0.8 1
x in half wavelengths
FIGURE 11.4 c*c Probabilities for the PIB butadiene wave functions. (From Trindle, C. and Shillady, D.,
Electronic Structure Modeling: Connections between Theory and Software, CRC Press, Boca Raton, FL, 2008.
With permission.)

the dot-product sense. The extension to multidimensional ‘‘Hilbert space’’ algebra is necessary in
quantum mechanics because there are many possible eigenfunctions but they are mutually orthog-
^ ^
onal in the sense that there is an integral over the product instead of i j ¼jijjjj cos(p=2) ¼ 0.
Students should be aware that there are really only about five or six problems that have known exact
solutions and although there is no proof that all the solutions form complete sets, there is no known
exception. As far as is known, a quantum mechanical solution to the Schrödinger equation
should=will have a set of solutions that form a complete set for any problem with the same boundary
conditions and there will be a set of corresponding eigenvalues. The set of orthogonal functions may
need to be normalized to the arbitrary certainty of 1 to reach the full condition of orthonormality.
This concept of a complete set of eigenfunctions and eigenvalues will be very useful for estimating
solutions to problems not yet solved.
Let us use this exactly solvable model to learn more about quantum mechanics. Note that we
could apply the Hamiltonian operator more than once and generate the value of the energy raised to
2
m
m
a power H op (H op c ) ¼ H op (E n c ) ¼ E n (H n c ) ¼ E c , in fact H c ¼ E c . This is so because
n
op n
n
n
n
n n
n
c n is an exact eigenfunction of H op and we say E n is a ‘‘good quantum number.’’ However there are
other quantities we would like to extract from the wave function. Return to the question of the most