Page 416 - Fair, Geyer, and Okun's Water and wastewater engineering : water supply and wastewater removal

JWCL344_ch11_357-397.qxd 8/2/10 9:01 PM Page 376

376 Chapter 11 Hydrology: Rainfall and Runoff
Table 11.2 Associations in Arithmetic and Geometric Probability Plots

Observed or Derived Magnitude
Observed or Derived
Frequency (%) Arithmetic Geometric
50 m m g
84.1 m + s m g * s g
15.9 m - s m g /s g

variable for some other functionally Gaussian normality. Observations that have a
lower limit at or near zero may be geometrically normal (log 0 q ).
Helpful and useful associations in arithmetic and geometric probability plots can be
listed as shown in Table 11.2.
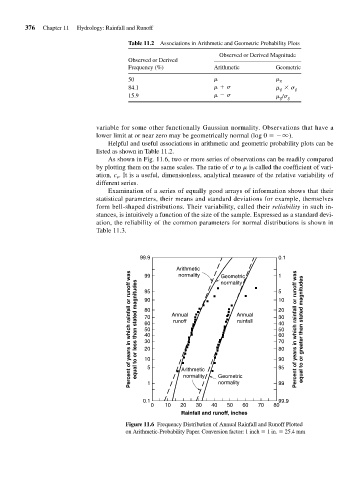
As shown in Fig. 11.6, two or more series of observations can be readily compared
by plotting them on the same scales. The ratio of s to m is called the coefficient of vari-
ation, c . It is a useful, dimensionless, analytical measure of the relative variability of
v
different series.
Examination of a series of equally good arrays of information shows that their
statistical parameters, their means and standard deviations for example, themselves
form bell-shaped distributions. Their variability, called their reliability in such in-
stances, is intuitively a function of the size of the sample. Expressed as a standard devi-
ation, the reliability of the common parameters for normal distributions is shown in
Table 11.3.

99.9 0.1
Arithmetic
99 normality Geometric 1
equal to or less than stated magnitudes Percent of years in which rainfall or runoff was 80 Annual Annual 20 Percent of years in which rainfall or runoff was equal to or greater than stated magnitudes
normality
5
95
10
90
30
70
runoff
rainfall
40
60
50
50
40
60
30
70
80
20
10
95
normality
normality
1 5 Arithmetic Geometric 90
99
0.1 99.9
0 10 20 30 40 50 60 70 80
Rainfall and runoff, inches
Figure 11.6 Frequency Distribution of Annual Rainfall and Runoff Plotted
on Arithmetic-Probability Paper. Conversion factor: 1 inch 1 in. 25.4 mm