Page 235 - Finite Element Modeling and Simulations with ANSYS Workbench

220 Finite Element Modeling and Simulation with ANSYS Workbench

y

x

z
y, v
y
yx
yz
zy xy
x
zx x, u
z xz

z, w

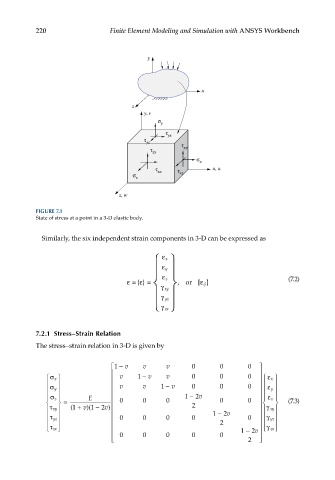
FIGURE 7.1
State of stress at a point in a 3-D elastic body.

Similarly, the six independent strain components in 3-D can be expressed as

 
ε x
ε  
ε y
z
ε = {} γ   , or ε [ ] (7.2)
ε =
ij
xy
 
γ yz
γ zx
 
7.2.1 Stress–Strain Relation
The stress–strain relation in 3-D is given by

1  − v v v 0 0 0 
 
 σ x   v v 1 − v v 0 0 0   ε x 
   v v 1 − v 0 0 0  
 σ y    ε y 



 σ z  E  1 − 2 v  ε z 



  =  0 0 0 2 0 0    (7.3)
 τ xy  (1 + v)(1 − 2 v)  1 − v 2   γ xy 
 τ yz   0 0 0 0 0  γ yz 
   2   
  τ zx     1 − v 2    γ zx  
 0 0 0 0 0 
 2 