Page 94 - Fluid Mechanics and Thermodynamics of Turbomachinery

Two-dimensional Cascades 75

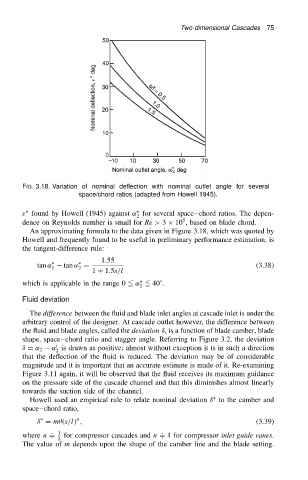
FIG. 3.18. Variation of nominal deflection with nominal outlet angle for several
space/chord ratios (adapted from Howell 1945).

Ł
Ł
ε found by Howell (1945) against ˛ for several space chord ratios. The depen-
2
5
dence on Reynolds number is small for Re > 3 ð 10 , based on blade chord.
An approximating formula to the data given in Figure 3.18, which was quoted by
Howell and frequently found to be useful in preliminary performance estimation, is
the tangent-difference rule:
1.55
Ł
Ł
tan ˛ 1 tan ˛ D (3.38)
2
1 C 1.5s/l
Ł
which is applicable in the range 0 5 ˛ 5 40 ° .
2
Fluid deviation
The difference between the fluid and blade inlet angles at cascade inlet is under the
arbitrary control of the designer. At cascade outlet however, the difference between
the fluid and blade angles, called the deviation υ, is a function of blade camber, blade
shape, space chord ratio and stagger angle. Referring to Figure 3.2, the deviation
0
˛ is drawn as positive; almost without exception it is in such a direction
υ D ˛ 2
2
that the deflection of the fluid is reduced. The deviation may be of considerable
magnitude and it is important that an accurate estimate is made of it. Re-examining
Figure 3.11 again, it will be observed that the fluid receives its maximum guidance
on the pressure side of the cascade channel and that this diminishes almost linearly
towards the suction side of the channel.
Ł
Howell used an empirical rule to relate nominal deviation υ to the camber and
space chord ratio,
Ł
n
υ D m .s/l/ , (3.39)
where n + 1 for compressor cascades and n + 1 for compressor inlet guide vanes.
2
The value of m depends upon the shape of the camber line and the blade setting.