Page 92 - Fluid Mechanics and Thermodynamics of Turbomachinery

Two-dimensional Cascades 73
velocity to outlet velocity, c max,s /c 2 . Lieblein found a correlation between the diffu-
sion ratio c max,s /c 2 and the wake momentum-thickness to chord ratio, 2 /l at the
reference incidence (mid-point of working range) for American NACA 65-(A 10 ) and
British C.4 circular-arc blades. The wake momentum-thickness, with the parameters
of the flow model in Figure 3.16 is defined as

Z
v v
υ s
2 D 1 dy. (3.30)
V V
υ p
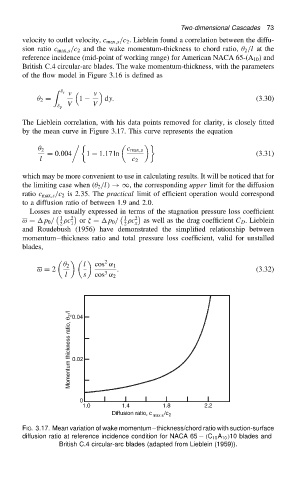
The Lieblein correlation, with his data points removed for clarity, is closely fitted
by the mean curve in Figure 3.17. This curve represents the equation

2 c max,s
D 0.004 1 1.17 ln (3.31)
l c 2

which may be more convenient to use in calculating results. It will be noticed that for
the limiting case when ( 2 /l/ !1, the corresponding upper limit for the diffusion
ratio c max,s /c 2 is 2.35. The practical limit of efficient operation would correspond
to a diffusion ratio of between 1.9 and 2.0.
Losses are usually expressed in terms of the stagnation pressure loss coefficient
ω D p 0 / 1 c 2 or D p 0 / 1 c 2 as well as the drag coefficient C D . Lieblein
2 1 2 x
and Roudebush (1956) have demonstrated the simplified relationship between
momentum thickness ratio and total pressure loss coefficient, valid for unstalled
blades,
2
2 l cos ˛ 1
ω D 2 . (3.32)
3
l s cos ˛ 2

FIG. 3.17. Mean variation of wake momentum thickness/chord ratio with suction-surface
diffusion ratio at reference incidence condition for NACA 65 .C 10 A 10 /10 blades and
British C.4 circular-arc blades (adapted from Lieblein (1959)).