Page 88 - Fluid Mechanics and Thermodynamics of Turbomachinery

Two-dimensional Cascades 69

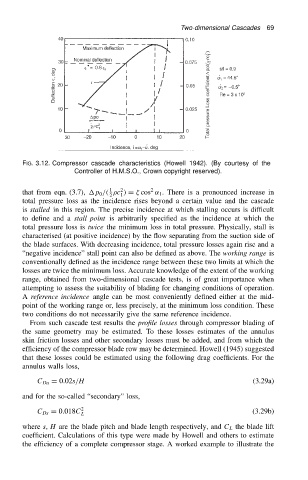
FIG. 3.12. Compressor cascade characteristics (Howell 1942). (By courtesy of the
Controller of H.M.S.O., Crown copyright reserved).

1
2
2
that from eqn. (3.7), p 0 /. c / D cos ˛ 1 . There is a pronounced increase in
2 1
total pressure loss as the incidence rises beyond a certain value and the cascade
is stalled in this region. The precise incidence at which stalling occurs is difficult
to define and a stall point is arbitrarily specified as the incidence at which the
total pressure loss is twice the minimum loss in total pressure. Physically, stall is
characterised (at positive incidence) by the flow separating from the suction side of
the blade surfaces. With decreasing incidence, total pressure losses again rise and a
“negative incidence” stall point can also be defined as above. The working range is
conventionally defined as the incidence range between these two limits at which the
losses are twice the minimum loss. Accurate knowledge of the extent of the working
range, obtained from two-dimensional cascade tests, is of great importance when
attempting to assess the suitability of blading for changing conditions of operation.
A reference incidence angle can be most conveniently defined either at the mid-
point of the working range or, less precisely, at the minimum loss condition. These
two conditions do not necessarily give the same reference incidence.
From such cascade test results the profile losses through compressor blading of
the same geometry may be estimated. To these losses estimates of the annulus
skin friction losses and other secondary losses must be added, and from which the
efficiency of the compressor blade row may be determined. Howell (1945) suggested
that these losses could be estimated using the following drag coefficients. For the
annulus walls loss,

C Da D 0.02s/H (3.29a)
and for the so-called “secondary” loss,

C Ds D 0.018C 2 (3.29b)
L
where s, H are the blade pitch and blade length respectively, and C L the blade lift
coefficient. Calculations of this type were made by Howell and others to estimate
the efficiency of a complete compressor stage. A worked example to illustrate the