Page 381 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 351

well not to rely on just one measure in deciding that motions are chaotic or otherwise.
Professor F.C. Moon made the point eloquently in a course he gave at Cornell, through
a parable, paraphrased here from memory. ‘If you see something that Zooks like a duck,
it does not necessarily mean that it is a duck. If, however, it also walks like a duck, it
swims like a duck, and it quacks like a duck, then it is much more likely to be one!’+
The experimental system was also studied analytically, initially by the simplest possible
model (PaYdoussis & Moon 1988; Paldoussis et aZ. 1989). As motions are relatively small
because of the constraining bars, the linear version of equation (5.39) is used as a first
approximation - i.e. equation (3.70) - apart from the forces associated with impacting.
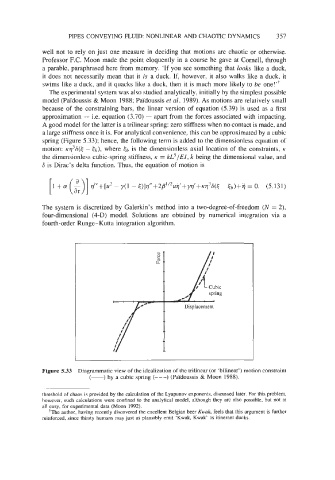
A good model for the latter is a trilinear spring: zero stiffness when no contact is made, and
a large stiffness once it is. For analytical convenience, this can be approximated by a cubic
spring (Figure 5.33); hence, the following term is added to the dimensionless equation of
motion: KQ~S($ - &,), where &, is the dimensionless axial location of the constraints, K
the dimensionless cubic-spring stiffness, K = kL5/EI, k being the dimensional value, and
S is Dirac’s delta function. Thus, the equation of motion is

The system is discretized by Galerkin’s method into a two-degree-of-freedom (N = 2),
four-dimensional (4-D) model. Solutions are obtained by numerical integration via a
fourth-order Runge- Kutta integration algorithm.

Figure 5.33 Diagrammatic view of the idealization of the trilinear (or ‘bilinear’) motion constraint
(-) by a cubic spring (---) (Pdidoussis & Moon 1988).

threshold of chaos is provided by the calculation of the Lyapunov exponents, discussed later. For this problem,
however, such calculations were confined to the analytical model, although they are also possible, but not at
all easy, for experimental data (Moon 1992).
+The author, having recently discovered the excellent Belgian beer Kwak, feels that this argument is further
reinforced, since thirsty humans may just as plausibly emit ‘Kwak, Kwak’ as itinerant ducks.