Page 380 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

356 SLENDER STRUCTURES AND AXIAL FLOW

4.6
-2.4 0.0 1.8
(C) W(V)
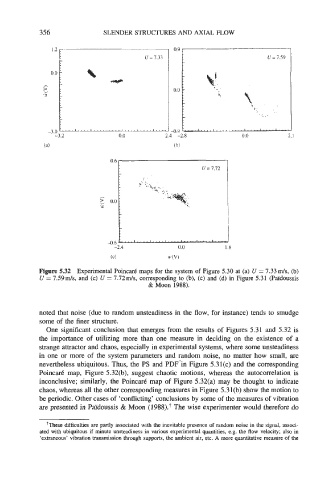
Figure 5.32 Experimental Poincar6 maps for the system of Figure 5.30 at (a) U = 7.33 ds, (b)
U = 7.59ds, and (c) U = 7.72ds, corresponding to (b), (c) and (d) in Figure 5.31 (Pdidoussis
& Moon 1988).

noted that noise (due to random unsteadiness in the flow, for instance) tends to smudge
some of the finer structure.
One significant conclusion that emerges from the results of Figures 5.31 and 5.32 is
the importance of utilizing more than one measure in deciding on the existence of a
strange attractor and chaos, especially in experimental systems, where some unsteadiness
in one or more of the system parameters and random noise, no matter how small, are
nevertheless ubiquitous. Thus, the PS and PDF'in Figure 5.31(c) and the corresponding
Poincark map, Figure 5.32(b), suggest chaotic motions, whereas the autocorrelation is
inconclusive; similarly, the Poincark map of Figure 5.32(a) may be thought to indicate
chaos, whereas all the other corresponding measures in Figure 5.31(b) show the motion to
be periodic. Other cases of 'conflicting' conclusions by some of the measures of vibration
are presented in Pdidoussis & Moon (1988).+ The wise experimenter would therefore do

+These difficulties are partly associated with the inevitable presence of random noise in the signal, associ-
ated with ubiquitous if minute unsteadiness in various experimental quantities, e.g. the flow velocity; also in
'extraneous' vibration transmission through supports, the ambient air, etc. A more quantitative measure of the