Page 440 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

412 SLENDER STRUCTURES AND AXIAL FLOW

p (p > 0.6) the pipe oscillates about a quasi-stationary deflected shape. (e) Again for
p > 0.6, the oscillation ceases being planar and becomes chaotic.
Quantitative comparisons with theory are undertaken for the principal resonance bound-
aries for a system at u = 0.9Oucf and 0.95~~- (Semler & Pdidoussis 1996; Figure 12).
The experimental boundaries are larger than the theoretical ones, similarly to the results
in Figure 4.32, and agreement with theory is similar. In the theoretical results no 'subcrit-
ical onset' of the resonance (a behaviour shown in Figure 5.63(c), for instance, but with
varying q) has been found; hence, the early appearance of resonance with increasing w
remains unexplainable.
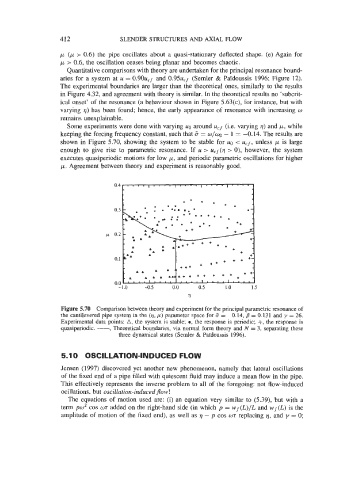
Some experiments were done with varying uo around ucf (i.e. varying q) and p, while
keeping the forcing frequency constant, such that 6 = w/og - 1 = -0.14. The results are
shown in Figure 5.70, showing the system to be stable for ug < u,f, unless p is large
enough to give rise to parametric resonance. If u > u,~(Q > 0), however, the system
executes quasiperiodic motions for low p, and periodic parametric oscillations for higher
p. Agreement between theory and experiment is reasonably good.

* . -
* .
>
+
-
-. . .A++ + ++ + + + +'
.
+
+-
0.1 2. a . + + +-
. .. IL + ++ + ++ +
- A & A . ..ah++++ + + + ++-
0.0 '.*m''-'*'*"'

Figure 5.70 Comparison between theory and experiment for the principal parametric resonance of
the cantilevered pipe system in the (q, p) parameter space for 6 = -0.14, B = 0.131 and y = 26.
Experimental data points: A, the system is stable; 0, the response is periodic; +, the response is
quasiperiodic. -, Theoretical boundaries, via normal form theory and N = 3, separating these
three dynamical states (Semler & Pai'doussis 1996).

5.1 0 OSCILLATION-INDUCED FLOW
Jensen (1 997) discovered yet another new phenomenon, namely that lateral oscillations
of the fixed end of a pipe filled with quiescent fluid may induce a mean flow in the pipe.
This effectively represents the inverse problem to all of the foregoing: not flow-induced
ocillations, but oscillation-induced $ow!
The equations of motion used are: (i) an equation very similar to (5.39), but with a
term pwz cos WT added on the right-hand side (in which p = wf(L)/L and wr(L) is the
amplitude of motion of the fixed end), as well as q - p cos WT replacing Q, and y = 0;