Page 442 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

414 SLENDER STRUCTURES AND AXIAL FLOW

22 I I I

0
0.01
0.005
0
"0 0.005 0.01 0 0 15
(a) Forcing amplitude, p
c

j= 1

I 1 I
0.0005 0.001 0.0015 0.002 0: )25
(b) Forcing amplitude, p
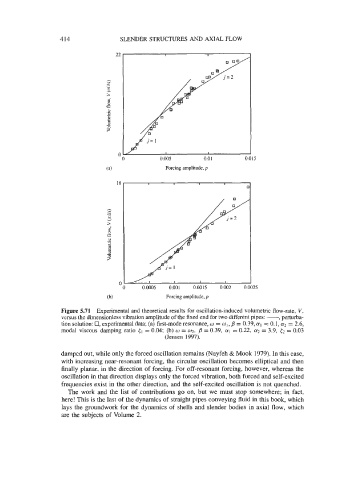
Figure 5.71 Experimental and theoretical results for oscillation-induced volumetric flow-rate, V,
versus the dimensionless vibration amplitude of the fixed end for two different pipes: -, perturba-
tion solution: 0, experimental data; (a) first-mode resonance, w = wl, ,9 = 0.39, al = 0.1, a2 = 2.6,
B
modal viscous damping ratio {I = 0.04; (b) w = ~2, = 0.39, a1 = 0.22, a2 = 3.9, {z = 0.03
(Jensen 1997).
damped out, while only the forced oscillation remains (Nayfeh & Mook 1979). In this case,
with increasing near-resonant forcing, the circular oscillation becomes elliptical and then
finally planar, in the direction of forcing. For off-resonant forcing, however, whereas the
oscillation in that direction displays only the forced vibration, both forced and self-excited
frequencies exist in the other direction, and the self-excited oscillation is not quenched.
The work and the list of contributions go on, but we must stop somewhere; in fact,
here! This is the last of the dynamics of straight pipes conveying fluid in this book, which
lays the groundwork for the dynamics of shells and slender bodies in axial flow, which
are the subjects of Volume 2.