Page 128 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C003.fm Page 108 Monday, May 23, 2005 5:42 PM

108 Fracture Mechanics: Fundamentals and Applications

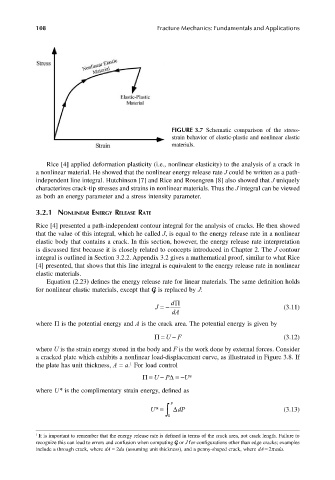
FIGURE 3.7 Schematic comparison of the stress-
strain behavior of elastic-plastic and nonlinear elastic
materials.

Rice [4] applied deformation plasticity (i.e., nonlinear elasticity) to the analysis of a crack in
a nonlinear material. He showed that the nonlinear energy release rate J could be written as a path-
independent line integral. Hutchinson [7] and Rice and Rosengren [8] also showed that J uniquely
characterizes crack-tip stresses and strains in nonlinear materials. Thus the J integral can be viewed
as both an energy parameter and a stress intensity parameter.

3.2.1 NONLINEAR ENERGY RELEASE RATE
Rice [4] presented a path-independent contour integral for the analysis of cracks. He then showed
that the value of this integral, which he called J, is equal to the energy release rate in a nonlinear
elastic body that contains a crack. In this section, however, the energy release rate interpretation
is discussed first because it is closely related to concepts introduced in Chapter 2. The J contour
integral is outlined in Section 3.2.2. Appendix 3.2 gives a mathematical proof, similar to what Rice
[4] presented, that shows that this line integral is equivalent to the energy release rate in nonlinear
elastic materials.
Equation (2.23) defines the energy release rate for linear materials. The same definition holds
for nonlinear elastic materials, except that G is replaced by J:
dΠ
J =− (3.11)
dA

where Π is the potential energy and A is the crack area. The potential energy is given by
Π= U − F (3.12)

where U is the strain energy stored in the body and F is the work done by external forces. Consider
a cracked plate which exhibits a nonlinear load-displacement curve, as illustrated in Figure 3.8. If
1
the plate has unit thickness, A = a. For load control
Π − U ∆ = = P − U *

where U* is the complimentary strain energy, defined as

U ∫ 0 P ∆ d* = P (3.13)

1 It is important to remember that the energy release rate is defined in terms of the crack area, not crack length. Failure to
recognize this can lead to errors and confusion when computing G or J for configurations other than edge cracks; examples
include a through crack, where dA = 2da (assuming unit thickness), and a penny-shaped crack, where dA = 2p ada.