Page 65 - Fundamentals of Communications Systems

Signals and Systems Review 2.17

In other words, a complex exponential of frequency f 1 can be represented in
the frequency domain with an impulse at f 1 . Consequently the Fourier trans-
form of a periodic signal is represented as
2πnt n
∞
∞
∞
X(f ) = x n exp j exp[− j 2π ft]dt = x nδ f − (2.68)
T T
−∞
n=−∞ n=−∞
Throughout the remainder of the text the spectrum of a periodic signal will
be plotted using lines with arrows at the top to represent the delta functions.
The bandwidth of periodic signals can be defined now by using the results of
Section 2.2.3.

EXAMPLE 2.26
Consider again the the cosine signal introduced in Example 2.5.
1 1
F(cos(2π f m t)) = δ( f − f m ) + δ( f + f m )
2 2
By all definitions the bandwidth of this signal is B = f m .

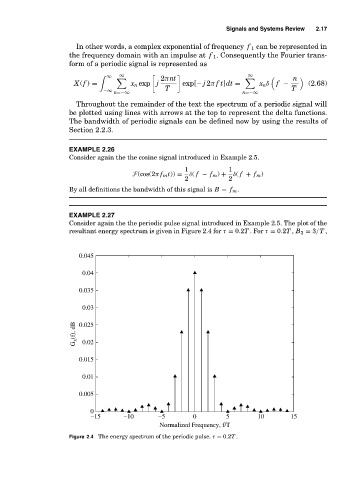
EXAMPLE 2.27
Consider again the the periodic pulse signal introduced in Example 2.5. The plot of the
resultant energy spectrum is given in Figure 2.4 for τ = 0.2T .For τ = 0.2T , B 3 = 3/T ,

0.045

0.04

0.035

0.03

G x (f), dB 0.025

0.02

0.015

0.01

0.005

0
−15 −10 −5 0 5 10 15
Normalized Frequency, f/T
Figure 2.4 The energy spectrum of the periodic pulse. τ = 0.2T .