Page 163 - Fundamentals of Probability and Statistics for Engineers

146 Fundamentals of Probability and Statistics for Engineers

x 2

y

x 1 +x 2 =y
R 2
x 1
y

2

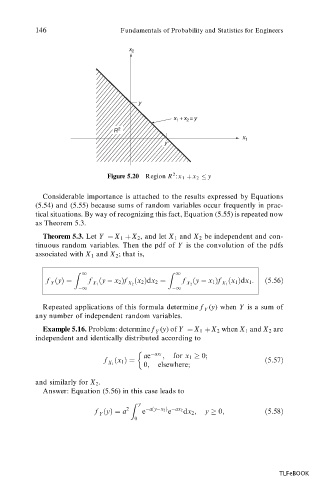
Figure 5.20 Region R : x 1 ‡ x 2 y
Considerable importance is attached to the results expressed by Equations
(5.54) and (5.55) because sums of random variables occur frequently in prac-
tical situations. By way of recognizing this fact, Equation (5.55) is repeated now
as Theorem 5.3.

Theorem 5.3. Let Y ˆ X 1 ‡ X 2 , and let X 1 and X 2 be independent and con-
tinuous random variables. Then the pdf of Y is the convolution of the pdfs
associated with X 1 and X 2 ; that is,
Z 1 Z 1
f y†ˆ f X 1 y
x 2 †f X 2 x 2 †dx 2 ˆ f X 2 y
x 1 †f X 1 x 1 †dx 1 : 5:56†
Y

1
1
Repeated applications of this formula determine f (y) when Y is a sum of
Y
any number of independent random variables.

Example 5.16. Problem: determine f (y) of Y ˆ X 1 ‡ X 2 when X 1 and X 2 are
Y
independent and identically distributed according to

ae
ax 1 ; for x 1 0;
f x 1 †ˆ 5:57†
X 1 0; elsewhere;
and similarly for X 2 .
Answer: Equation (5.56) in this case leads to
Z y
f y†ˆ a 2 e
a y
x 2 †
ax 2 dx 2 ; y 0; 5:58†
e
Y
0

TLFeBOOK