Page 73 - Fundamentals of Probability and Statistics for Engineers

56 Fundamentals of Probability and Statistics for Engineers

density function (jpdf) of two random variables, X and Y , is defined by the
partial derivative

2
q F XY x; y†
f XY x; y†ˆ : 3:24†
qxqy
Since F XY (x, y) is monotone nondecreasing in both x and y, f (x, y) is
XY
nonnegative for all x and y. We also see from Equation (3.24) that

y x
Z Z
F XY x; y† P X x \ Y y†ˆ f u; v†dudv: 3:25†
XY
1 1
Moreover, with x 1 < x 2 , and y 1 < y 2 ,

Z Z
y 2 x 2
P x 1 < X x 2 \ y 1 < Y y 2 †ˆ f XY x; y†dxdy: 3:26†
y 1 x 1
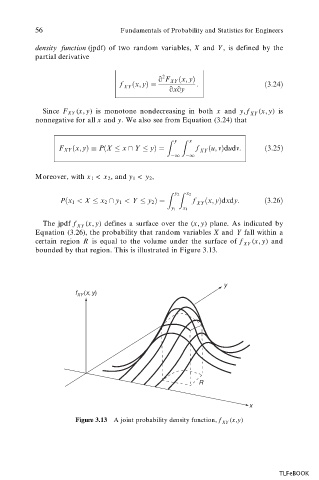
The jpdf f XY (x, y) defines a surface over the (x, y) plane. As indicated by
Equation (3.26), the probability that random variables X and Y fall within a
certain region R is equal to the volume under the surface of f XY (x, y) and
bounded by that region. This is illustrated in Figure 3.13.

y
f XY (x, y)

R

x
Figure 3.13 A joint probability density function, f XY (x,y)

TLFeBOOK