Page 393 - Fundamentals of Reservoir Engineering
P. 393
NATURAL WATER INFLUX 328
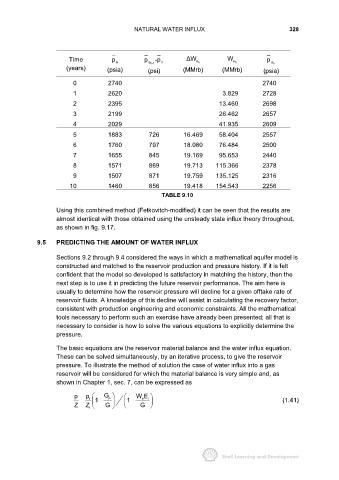
Time p n p a n-1 -p n ∆W n e W n e p a n
(years) (psia) (psi) (MMrb) (MMrb) (psia)
0 2740 2740
1 2620 3.829 2728
2 2395 13.460 2698
3 2199 26.462 2657
4 2029 41.935 2609
5 1883 726 16.469 58.404 2557
6 1760 797 18.080 76.484 2500
7 1655 845 19.169 95.653 2440
8 1571 869 19.713 115.366 2378
9 1507 871 19.759 135.125 2316
10 1460 856 19.418 154.543 2256
TABLE 9.10
Using this combined method (Fetkovitch-modified) it can be seen that the results are
almost identical with those obtained using the unsteady state influx theory throughout,
as shown in fig. 9.17.
9.5 PREDICTING THE AMOUNT OF WATER INFLUX
Sections 9.2 through 9.4 considered the ways in which a mathematical aquifer model is
constructed and matched to the reservoir production and pressure history. If it is felt
confident that the model so developed is satisfactory in matching the history, then the
next step is to use it in predicting the future reservoir performance. The aim here is
usually to determine how the reservoir pressure will decline for a given offtake rate of
reservoir fluids. A knowledge of this decline will assist in calculating the recovery factor,
consistent with production engineering and economic constraints. All the mathematical
tools necessary to perform such an exercise have already been presented; all that is
necessary to consider is how to solve the various equations to explicitly determine the
pressure.
The basic equations are the reservoir material balance and the water influx equation.
These can be solved simultaneously, by an iterative process, to give the reservoir
pressure. To illustrate the method of solution the case of water influx into a gas
reservoir will be considered for which the material balance is very simple and, as
shown in Chapter 1, sec. 7, can be expressed as
p p G WE
p
e
i
i
= 1− 1− (1.41)
Z Z i G G