Page 395 - Fundamentals of Reservoir Engineering

NATURAL WATER INFLUX 330

Time step = n

k = 1

k n2
−
p p G E i
n p
i
1 U
= 1 − − ∆ p W (T − t )
D
D
D
j

Z n Z i G j=α 0 i G
p k n
n2 U
−
k
W k n e = U ∆ p W (T − t ) + (p n 2 − p )W (T − t D )
D
j
D
n
j D
D
D
−
−
j0 2 n 1
=
k
W k n e p = p k n -1
n
n=n+1 k=k+ 1
k k E
p p G n p W n e i
i
= 1 − 1 −
Z n Z i G G
p k n
k = 1
k
- k k − 1 +
p n − p n − TOL

k = iteration counter
TOL = tolerance pressure
difference (psi)

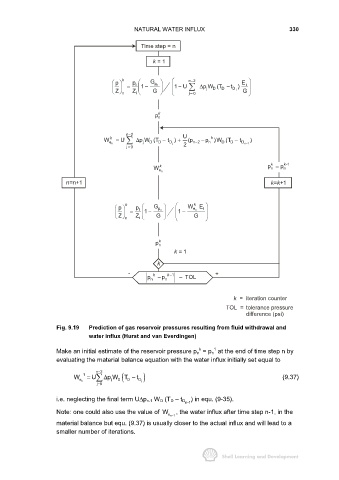
Fig. 9.19 Prediction of gas reservoir pressures resulting from fluid withdrawal and
water influx (Hurst and van Everdingen)

k
1
Make an initial estimate of the reservoir pressure p n = p n at the end of time step n by
evaluating the material balance equation with the water influx initially set equal to
n2
−
W e 1 = U ∆ p W T − t j D ) (9.37)
D
j
( D
n
j0
=
i.e. neglecting the final term U∆p n-1 W D (T D – t D ) in equ. (9-35).
n-1
Note: one could also use the value of W e n1 , the water influx after time step n-1, in the
−
material balance but equ. (9.37) is usually closer to the actual influx and will lead to a
smaller number of iterations.