Page 237 - Fundamentals of The Finite Element Method for Heat and Fluid Flow

CONVECTION HEAT TRANSFER
6 229

5

4
Vertical velocity 3

2

1

0
0 0.2 0.4 0.6 0.8 1
Horizontal distance
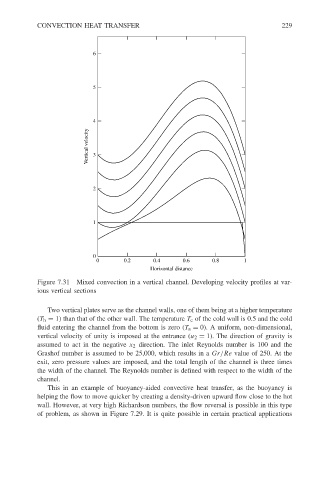
Figure 7.31 Mixed convection in a vertical channel. Developing velocity profiles at var-
ious vertical sections

Two vertical plates serve as the channel walls, one of them being at a higher temperature
(T h = 1) than that of the other wall. The temperature T c of the cold wall is 0.5 and the cold
fluid entering the channel from the bottom is zero (T a = 0). A uniform, non-dimensional,
vertical velocity of unity is imposed at the entrance (u 2 = 1). The direction of gravity is
assumed to act in the negative x 2 direction. The inlet Reynolds number is 100 and the
Grashof number is assumed to be 25,000, which results in a Gr/Re value of 250. At the
exit, zero pressure values are imposed, and the total length of the channel is three times
the width of the channel. The Reynolds number is defined with respect to the width of the
channel.
This in an example of buoyancy-aided convective heat transfer, as the buoyancy is
helping the flow to move quicker by creating a density-driven upward flow close to the hot
wall. However, at very high Richardson numbers, the flow reversal is possible in this type
of problem, as shown in Figure 7.29. It is quite possible in certain practical applications