Page 36 - Fundamentals of The Finite Element Method for Heat and Fluid Flow

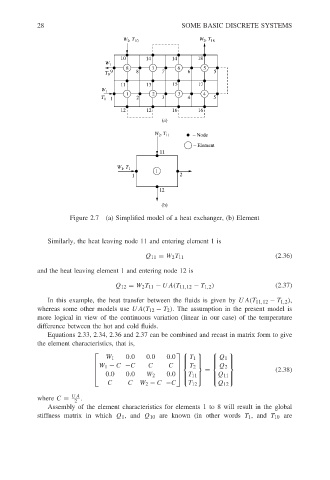
28
W 2 , T 18
10 W 2 , T 10 14 14 SOME BASIC DISCRETE SYSTEMS
18
W 1
8 7 6 5
9 8 7 6 5
T 9
11 13 15 17
W 1
1 2 3 4
T 1 1 2 3 4 5
12 12 16 16
(a)
W 2 , T 11 − Node
− Element
11

W 1 , T 1
1
1 2
12
(b)

Figure 2.7 (a) Simplified model of a heat exchanger, (b) Element

Similarly, the heat leaving node 11 and entering element 1 is

Q 11 = W 2 T 11 (2.36)
and the heat leaving element 1 and entering node 12 is

Q 12 = W 2 T 11 − UA(T 11,12 − T 1,2 ) (2.37)
In this example, the heat transfer between the fluids is given by UA(T 11,12 − T 1,2 ),
whereas some other models use UA(T 12 − T 2 ). The assumption in the present model is
more logical in view of the continuous variation (linear in our case) of the temperature
difference between the hot and cold fluids.
Equations 2.33, 2.34, 2.36 and 2.37 can be combined and recast in matrix form to give
the element characteristics, that is,
     
W 1 0.0 0.0 0.0
 T 1   Q 1 
   
W 1 − C −C C C    
  T 2 Q 2
  = (2.38)
0.0 0.0 0.0
 W 2  T 11 Q 11
   
C C W 2 − C −C  T 12   Q 12 
UA
where C = .
2
Assembly of the element characteristics for elements 1 to 8 will result in the global
stiffness matrix in which Q 1 ,and Q 10 are known (in other words T 1 ,and T 10 are