Page 291 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

246 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

Exit flow C o

δ
Eddies
Convection

Raw water flow
Reactor Reactor
Alum Alum
(a) (b) (c)
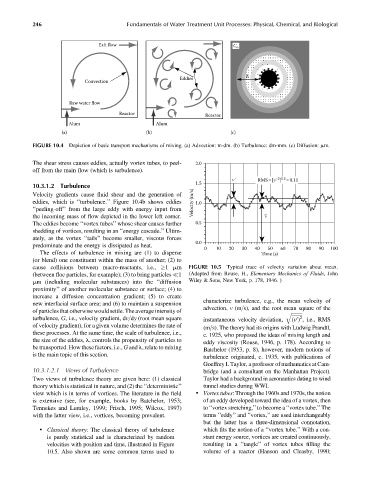
FIGURE 10.4 Depiction of basic transport mechanisms of mixing. (a) Advection: m-dm. (b) Turbulence: dm-mm. (c) Diffusion: mm.

The shear stress causes eddies, actually vortex tubes, to peel- 2.0
off from the main flow (which is turbulence).
2 0.5
v΄ RMS=[v΄ ] =0.11
1.5
10.3.1.2 Turbulence
Velocity gradients cause fluid shear and the generation of
eddies, which is ‘‘turbulence.’’ Figure 10.4b shows eddies Velocity (m/s) 1.0
‘‘peeling-off’’ from the large eddy with energy input from
the incoming mass of flow depicted in the lower left corner. –
v
The eddies become ‘‘vortex tubes’’ whose shear causes further 0.5
shedding of vortices, resulting in an ‘‘energy cascade.’’ Ultim-
ately, as the vortex ‘‘tails’’ become smaller, viscous forces
0.0
predominate and the energy is dissipated as heat.
0 10 20 30 40 50 60 70 80 90 100
The effects of turbulence in mixing are (1) to disperse Time (s)
(or blend) one constituent within the mass of another; (2) to
cause collisions between macro-reactants, i.e., 1 mm FIGURE 10.5 Typical trace of velocity variation about mean.
(between floc particles, for example); (3) to bring particles 1 (Adapted from Rouse, H., Elementary Mechanics of Fluids, John
mm (including molecular substances) into the ‘‘diffusion Wiley & Sons, New York, p. 178, 1946. )
proximity’’ of another molecular substance or surface; (4) to
increase a diffusion concentration gradient; (5) to create
characterize turbulence, e.g., the mean velocity of
new interfacial surface area; and (6) to maintain a suspension
advection, v (m=s), and the root mean square of the
of particles that otherwise would settle. The average intensity of q ffiffiffiffiffiffiffiffiffi
turbulence, G, i.e., velocity gradient, dv=dy (root mean square instantaneous velocity deviation, (v ) ,i.e.,RMS
0 2
of velocity gradient), for a given volume determines the rate of (m=s). The theory had its origins with Ludwig Prandtl,
these processes. At the same time, the scale of turbulence, i.e., c. 1925, who proposed the ideas of mixing length and
the size of the eddies, l, controls the propensity of particles to eddy viscosity (Rouse, 1946, p. 178). According to
be transported. How these factors, i.e., G and l, relate to mixing Batchelor (1953, p. 8), however, modern notions of
is the main topic of this section. turbulence originated, c. 1935, with publications of
Goeffrey I. Taylor, a professor of mathematics at Cam-
10.3.1.2.1 Views of Turbulence bridge (and a consultant on the Manhattan Project).
Two views of turbulence theory are given here: (1) classical Taylor had a background in aeronautics dating to wind
theory which is statistical in nature, and (2) the ‘‘deterministic’’ tunnel studies during WWI.
view which is in terms of vortices. The literature in the field . Vortex tubes: Through the 1960s and 1970s, the notion
is extensive (see, for example, books by Batchelor, 1953; of an eddy developed toward the idea of a vortex, then
Tennekes and Lumley, 1999; Frisch, 1995; Wilcox, 1997) to ‘‘vortex stretching,’’ to become a ‘‘vortex tube.’’ The
with the latter view, i.e., vortices, becoming prevalent. terms ‘‘eddy’’ and ‘‘vortex,’’ are used interchangeably
but the latter has a three-dimensional connotation,
. Classical theory: The classical theory of turbulence which fits the notion of a ‘‘vortex tube.’’ With a con-
is purely statistical and is characterized by random stant energy source, vortices are created continuously,
velocities with position and time, illustrated in Figure resulting in a ‘‘tangle’’ of vortex tubes filling the
10.5. Also shown are some common terms used to volume of a reactor (Hanson and Cleasby, 1990;