Page 294 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

Mixing 249

previously (i.e., as in Figure 10.6). Vortex sizes range from 1 1
ð
the dimension of the disturbance to the ‘‘Kolmogorov micro- u i (x)u i (x) ¼ E(k)dk (10:12)
2
scale’’ (Box 10.2); which is micrometers in size. For eddies 0
having this micrometer-scale size, their energy is dissipated as
viscous shear. Each vortex tube has a different amount of and
kinetic energy and the distribution of energy with size is
called the ‘‘energy spectrum’’ (Stenquist and Kaufman, 1
(10:13)
1972, p. 11). In the parlance of theoreticians, the reciprocal k l
of the eddy size in meters is called the ‘‘wave number.’’
The total kinetic energy per unit mass of fluid is (Batchelor, where
1953, p. 36) u i is the velocity of eddy i (m=s)
k is the wave number (1=m)
l is the diameter of vortex tube (m)
E(k) is the energy as function of wave length, i.e., the
2
‘‘energy spectrum’’ (N m =kg)
BOX 10.2 KOLMOGOROV’S
1
u
CONTRIBUTION TO TURBULENCE THEORY 2 i (x)u i (x) is the mean kinetic energy of all eddies collect-
3
2
2
ively (m =s ), which is same as (N m =kg)
According to A. N. Kolmogorov’s 1941 paper, there is a
range of high frequencies where the turbulence is statis-
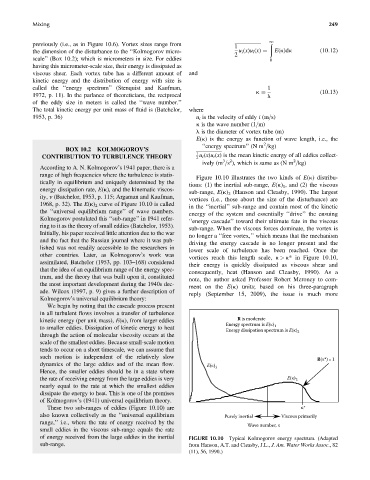
Figure 10.10 illustrates the two kinds of E(k) distribu-
tically in equilibrium and uniquely determined by the
tions: (1) the inertial sub-range, E(k) 1 , and (2) the viscous
energy dissipation rate, E(k), and the kinematic viscos-
sub-range, E(k) 2 (Hanson and Cleasby, 1990). The largest
ity, n (Batchelor, 1953, p. 115; Argaman and Kaufman,
vortices (i.e., those about the size of the disturbance) are
1968, p. 32). The E(k) 2 curve of Figure 10.10 is called
in the ‘‘inertial’’ sub-range and contain most of the kinetic
the ‘‘universal equilibrium range’’ of wave numbers.
energy of the system and essentially ‘‘drive’’ the ensuing
Kolmogorov postulated this ‘‘sub-range’’ in 1941 refer-
‘‘energy cascade’’ toward their ultimate fate in the viscous
ring to it as the theory of small eddies (Batchelor, 1953).
sub-range. When the viscous forces dominate, the vortex is
Initially, his paper received little attention due to the war
no longer a ‘‘free vortex,’’ which means that the mechanism
and the fact that the Russian journal where it was pub-
driving the energy cascade is no longer present and the
lished was not readily accessible to the researchers in
lower scale of turbulence has been reached. Once the
other countries. Later, as Kolmogorov’s work was
vortices reach this length scale, k > k* in Figure 10.10,
assimilated, Batchelor (1953, pp. 103–168) considered
their energy is quickly dissipated as viscous shear and
that the idea of an equilibrium range of the energy spec-
consequently, heat (Hanson and Cleasby, 1990). As a
trum, and the theory that was built upon it, constituted
note, the author asked Professor Robert Meroney to com-
the most important development during the 1940s dec-
ment on the E(k) units; based on his three-paragraph
ade. Wilcox (1997, p. 9) gives a further description of
reply (September 15, 2009), the issue is much more
Kolmogorov’s universal equilibrium theory:
We begin by noting that the cascade process present
in all turbulent flows involves a transfer of turbulence
kinetic energy (per unit mass), E(k), from larger eddies R is moderate
Energy spectrum is E(κ) 1
to smaller eddies. Dissipation of kinetic energy to heat
Energy dissipation spectrum is E(κ) 2
through the action of molecular viscosity occurs at the
scale of the smallest eddies. Because small-scale motion
tends to occur on a short timescale, we can assume that
such motion is independent of the relatively slow
R(κ*)=1
dynamics of the large eddies and of the mean flow.
E(κ) 1
Hence, the smaller eddies should be in a state where
the rate of receiving energy from the large eddies is very E(κ) 2
nearly equal to the rate at which the smallest eddies
dissipate the energy to heat. This is one of the premises
of Kolmogorov’s (1941) universal equilibrium theory.
These two sub-ranges of eddies (Figure 10.10) are κ*
also known collectively as the ‘‘universal equilibrium Purely inertial Viscous primarily
range,’’ i.e., where the rate of energy received by the
Wave number, κ
small eddies in the viscous sub-range equals the rate
of energy received from the large eddies in the inertial FIGURE 10.10 Typical Kolmogorov energy spectrum. (Adapted
sub-range. from Hanson, A.T. and Cleasby, J.L., J. Am. Water Works Assoc., 82
(11), 56, 1990.)