Page 775 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

730 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

Reactor S n

Q S Q Clarifier Q
X
S o V S pond S S
X o X X e

0
FIGURE 23.4 Aerated lagoon schematic. 0 Z

Q S X
Q S o X o
emissions have been considered not acceptable. Separating
the cells and sending to a digester would be a more contem-
porary solution.
The mass balance relations are the same as for conven- ΔZ
tional activated sludge, except that W ¼ 0. The associated
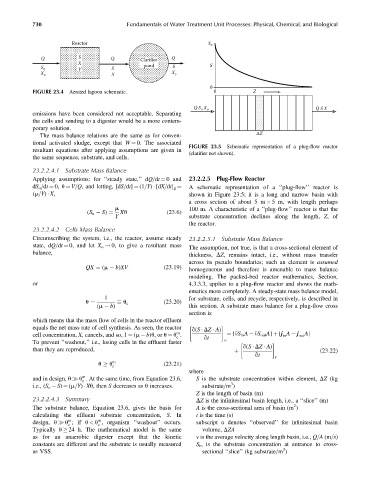
FIGURE 23.5 Schematic representation of a plug-flow reactor
resultant equations after applying assumptions are given in
(clarifier not shown).
the same sequence, substrate, and cells.
23.2.2.4.1 Substrate Mass Balance
Applying assumptions: for ‘‘steady state,’’ dQ=dt ¼ 0 and 23.2.2.5 Plug-Flow Reactor
A schematic representation of a ‘‘plug-flow’’ reactor is
dS o =dt ¼ 0, u ¼ V=Q, and letting, [dS=dt] ¼ (1=Y) [dX=dt] g ¼
(m=Y) X, shown in Figure 23.5; it is a long and narrow basin with
a cross section of about 5 m 5 m, with length perhaps
m 100 m. A characteristic of a ‘‘plug-flow’’ reactor is that the
Xu (23:6)
Y substrate concentration declines along the length, Z,of
(S o S) ¼
the reactor.
23.2.2.4.2 Cells Mass Balance
Circumscribing the system, i.e., the reactor, assume steady 23.2.2.5.1 Substrate Mass Balance
state, dQ=dt ¼ 0, and let X o ! 0, to give a resultant mass
The assumption, not true, is that a cross-sectional element of
balance,
thickness, DZ, remains intact, i.e., without mass transfer
across its pseudo boundaries; such an element is assumed
QX ¼ (m b)XV (23:19)
homogeneous and therefore is amenable to mass balance
modeling. The packed-bed reactor mathematics, Section,
or 4.3.3.3, applies to a plug-flow reactor and shows the math-
ematics more completely. A steady-state mass balance model,
1 for substrate, cells, and recycle, respectively, is described in
u c (23:20)
(m b) this section. A substrate mass balance for a plug-flow cross
u ¼
section is
which means that the mass flow of cells in the reactor effluent
equals the net mass rate of cell synthesis. As seen, the reactor q(S DZ A)
m
cell concentration, X, cancels, and so, 1 ¼ (m b)u,or u ¼ u . ¼ [ vS in A vS out A] þ [j A j A]
in
out
c qt
To prevent ‘‘washout,’’ i.e., losing cells in the effluent faster o
q(S DZ A)
than they are reproduced, (23:22)
qt
þ
r
u u m (23:21)
c
where
m
and in design, u u . At the same time, from Equation 23.6, S is the substrate concentration within element, DZ (kg
c
3
i.e., (S o S) ¼ (m=Y) Xu, then S decreases as u increases. substrate=m )
Z is the length of basin (m)
23.2.2.4.3 Summary DZ is the infinitesimal basin length, i.e., a ‘‘slice’’ (m)
2
The substrate balance, Equation 23.6, gives the basis for A is the cross-sectional area of basin (m )
calculating the effluent substrate concentration, S.In t is the time (s)
m
m
design, u u ;if u < u , organism ‘‘washout’’ occurs. subscript o denotes ‘‘observed’’ for infinitesimal basin
c c
Typically u 24 h. The mathematical model is the same volume, DZA
as for an anaerobic digester except that the kinetic v is the average velocity along length basin, i.e., Q=A (m=s)
constants are different and the substrate is usually measured S in is the substrate concentration at entrance to cross-
3
as VSS. sectional ‘‘slice’’ (kg substrate=m )