Page 121 - Geothermal Energy Renewable Energy and The Environment

Exploring for Geothermal Systems 107

NW Possible flow paths SE
Mangakino Kaingaroa
caldera plateau Ωm
0 3000
1000
300
Depth (km) 10 100

20 30
10
3
km
Possible magma body 0 10
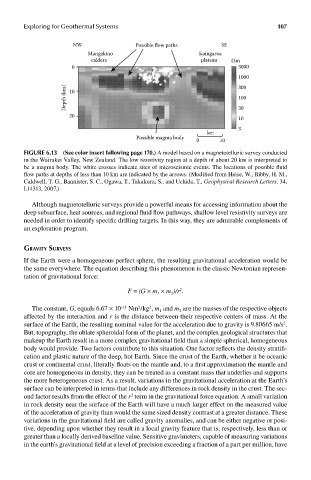
FIGUre 6.13 (See color insert following page 17.0..) A model based on a magnetotelluric survey conducted
in the Wairakei Valley, New Zealand. The low resistivity region at a depth of about 20 km is interpreted to
be a magma body. The white crosses indicate sites of microseismic events. The locations of possible fluid
flow paths at depths of less than 10 km are indicated by the arrows. (Modified from Heise, W., Bibby, H. M.,
Caldwell, T. G., Bannister, S. C., Ogawa, T., Takakura, S., and Uchida, T., Geophysical Research Letters, 34,
L14313, 2007.)

Although magnetotelluric surveys provide a powerful means for accessing information about the
deep subsurface, heat sources, and regional fluid flow pathways, shallow level resistivity surveys are
needed in order to identify specific drilling targets. In this way, they are admirable complements of
an exploration program.

GraviTy surveys
If the Earth were a homogeneous perfect sphere, the resulting gravitational acceleration would be
the same everywhere. The equation describing this phenomenon is the classic Newtonian represen-
tation of gravitational force:

2
F = (G × m × m )/r .
1
2
2
2
−11
The constant, G, equals 6.67 × 10 Nm /kg , m and m are the masses of the respective objects
2
1
affected by the interaction and r is the distance between their respective centers of mass. At the
2
surface of the Earth, the resulting nominal value for the acceleration due to gravity is 9.80665 m/s .
But, topography, the oblate spheroidal form of the planet, and the complex geological structures that
makeup the Earth result in a more complex gravitational field than a simple spherical, homogeneous
body would provide. Two factors contribute to this situation. One factor reflects the density stratifi-
cation and plastic nature of the deep, hot Earth. Since the crust of the Earth, whether it be oceanic
crust or continental crust, literally floats on the mantle and, to a first approximation the mantle and
core are homogeneous in density, they can be treated as a constant mass that underlies and supports
the more heterogeneous crust. As a result, variations in the gravitational acceleration at the Earth’s
surface can be interpreted in terms that include any differences in rock density in the crust. The sec-
ond factor results from the effect of the r term in the gravitational force equation. A small variation
2
in rock density near the surface of the Earth will have a much larger effect on the measured value
of the acceleration of gravity than would the same sized density contrast at a greater distance. These
variations in the gravitational field are called gravity anomalies, and can be either negative or posi-
tive, depending upon whether they result in a local gravity feature that is, respectively, less than or
greater than a locally derived baseline value. Sensitive gravimeters, capable of measuring variations
in the earth’s gravitational field at a level of precision exceeding a fraction of a part per million, have