Page 239 - Hardware Implementation of Finite-Field Arithmetic

m
Operations over GF (2 )—Polynomial Bases 219

7.6.4 Trinomials
m
m
k
Let f(x) = x + x + 1 be an irreducible trinomial generating GF(2 ). The
trinomial f(x) has only three nonzero coefficients and no other binary
irreducible polynomial has fewer nonzero coefficients. Irreducible
trinomials have drawn significant attention because polynomials with a
low Hamming weight can reduce the complexity of finite field arithmetic
([HK99], [HK00], [IST06], [RH04], [SK99], [Wu02], [ZP01]). Furthermore,
irreducible trinomials are abundant for every degree m [Ser98].
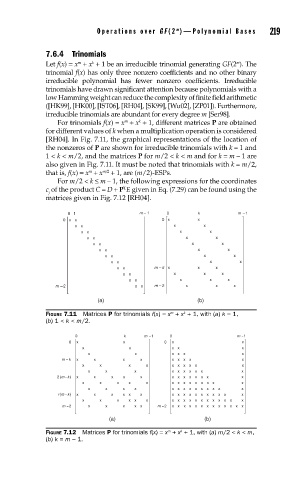
For trinomials f(x) = x + x + 1, different matrices P are obtained
m
k
for different values of k when a multiplication operation is considered
[RH04]. In Fig. 7.11, the graphical representations of the location of
the nonzeros of P are shown for irreducible trinomials with k = 1 and
1 < k < m/2, and the matrices P for m/2 < k < m and for k = m – 1 are
also given in Fig. 7.11. It must be noted that trinomials with k = m/2,
m
m/2
that is, f(x) = x + x + 1, are (m/2)-ESPs.
For m/2 < k ≤ m – 1, the following expressions for the coordinates
T
c of the product C = D + P E given in Eq. (7.29) can be found using the
j
matrices given in Fig. 7.12 [RH04].
m – 1

(a) (b)
k
m
FIGURE 7.11 Matrices P for trinomials f(x) = x + x + 1, with (a) k = 1,
(b) 1 < k < m/2.

(a) (b)
FIGURE 7.12 Matrices P for trinomials f(x) = x + x + 1, with (a) m/2 < k < m,
k
m
(b) k = m − 1.