Page 69 - Hardware Implementation of Finite-Field Arithmetic

52 Cha pte r T w o

xx1: = x(383..320) & x(383..320) & x(383..320)
xx2: = x(319..256) & x(319..256) & 00...00
x (255..192) &
xx1(191..0) xx2(191..0) x (191..0) x (255..192)
0 0 0

193-bit adder 193-bit adder

0 0

194-bit adder

s (193..0)

minus_3p minus_2p minus_p
0 0 0 0 0

195-bit adder 194-bit adder 193-bit adder

z1(192)
z2(193) z1(191:0) s (191..0)
0 1
z2(191:0)
z3 (194)
0 1
z3(191:0)
0 1

x mod p192
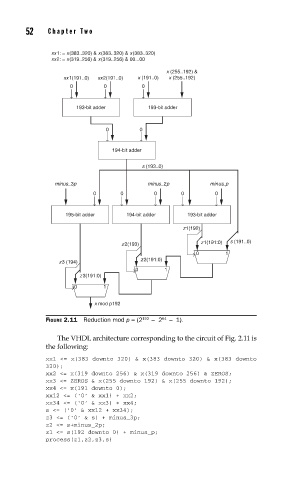
FIGURE 2.11 Reduction mod p = (2 192 − 2 − 1).
64
The VHDL architecture corresponding to the circuit of Fig. 2.11 is
the following:
xx1 <= x(383 downto 320) & x(383 downto 320) & x(383 downto
320);
xx2 <= x(319 downto 256) & x(319 downto 256) & ZEROS;
xx3 <= ZEROS & x(255 downto 192) & x(255 downto 192);
xx4 <= x(191 downto 0);
xx12 <= (‘0’ & xx1) + xx2;
xx34 <= (‘0’ & xx3) + xx4;
s <= (‘0’ & xx12 + xx34);
z3 <= (‘0’ & s) + minus_3p;
z2 <= s+minus_2p;
z1 <= s(192 downto 0) + minus_p;
process(z1,z2,z3,s)