Page 74 - Hardware Implementation of Finite-Field Arithmetic

mod m Reduction 57

ik
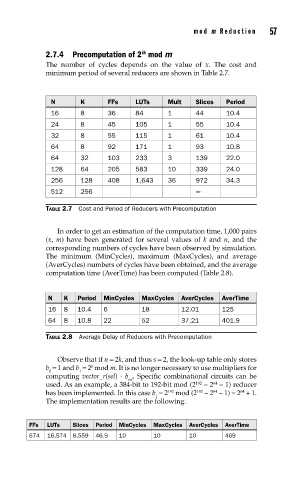
2.7.4 Precomputation of 2 mod m
The number of cycles depends on the value of x. The cost and
minimum period of several reducers are shown in Table 2.7.

N K FFs LUTs Mult Slices Period
16 8 36 84 1 44 10.4
24 8 45 105 1 55 10.4
32 8 55 115 1 61 10.4
64 8 92 171 1 93 10.8
64 32 103 233 3 139 22.0
128 64 205 583 10 339 24.0
256 128 408 1,643 36 972 34.3
512 256 ∞

TABLE 2.7 Cost and Period of Reducers with Precomputation

In order to get an estimation of the computation time, 1,000 pairs
(x, m) have been generated for several values of k and n, and the
corresponding numbers of cycles have been observed by simulation.
The minimum (MinCycles), maximum (MaxCycles), and average
(AverCycles) numbers of cycles have been obtained, and the average
computation time (AverTime) has been computed (Table 2.8).

N K Period MinCycles MaxCycles AverCycles AverTime
16 8 10.4 6 18 12.01 125
64 8 10.8 22 52 37.21 401.9

TABLE 2.8 Average Delay of Reducers with Precomputation

Observe that if n = 2k, and thus s = 2, the look-up table only stores
k
b = 1 and b = 2 mod m. It is no longer necessary to use multipliers for
0 1
computing vector_r(sel) . b . Specific combinational circuits can be
sel
64
192
used. As an example, a 384-bit to 192-bit mod (2 − 2 − 1) reducer
64
192
192
64
has been implemented. In this case b = 2 mod (2 − 2 − 1) = 2 + 1.
1
The implementation results are the following.
FFs LUTs Slices Period MinCycles MaxCycles AverCycles AverTime
674 16,574 8,559 46.9 10 10 10 469