Page 75 - Hardware Implementation of Finite-Field Arithmetic

58 Cha pte r T w o

2.7.5 Barrett Reduction
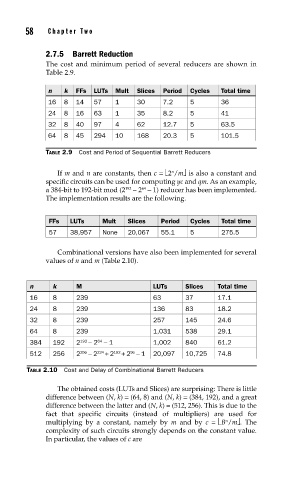
The cost and minimum period of several reducers are shown in
Table 2.9.

n k FFs LUTs Mult Slices Period Cycles Total time
16 8 14 57 1 30 7.2 5 36
24 8 16 63 1 35 8.2 5 41
32 8 40 97 4 62 12.7 5 63.5
64 8 45 294 10 168 20.3 5 101.5

TABLE 2.9 Cost and Period of Sequential Barrett Reducers

If m and n are constants, then c = ⎣2 /m⎦ is also a constant and
n
specific circuits can be used for computing yc and qm. As an example,
192
a 384-bit to 192-bit mod (2 − 2 − 1) reducer has been implemented.
64
The implementation results are the following.
FFs LUTs Mult Slices Period Cycles Total time
57 38,957 None 20,067 55.1 5 275.5

Combinational versions have also been implemented for several
values of n and m (Table 2.10).

n k M LUTs Slices Total time
16 8 239 63 37 17.1
24 8 239 136 83 18.2
32 8 239 257 145 24.6
64 8 239 1,031 538 29.1
64
384 192 2 192 − 2 − 1 1,002 840 61.2
256
96
512 256 2 − 2 224 + 2 192 + 2 − 1 20,097 10,725 74.8
TABLE 2.10 Cost and Delay of Combinational Barrett Reducers

The obtained costs (LUTs and Slices) are surprising: There is little
difference between (N, k) = (64, 8) and (N, k) = (384, 192), and a great
difference between the latter and (N, k) = (512, 256). This is due to the
fact that specific circuits (instead of multipliers) are used for
n
multiplying by a constant, namely by m and by c =⎣B /m⎦. The
complexity of such circuits strongly depends on the constant value.
In particular, the values of c are