Page 319 - High Power Laser Handbook

288 So l i d - S t at e La s e r s Heat-Capacity Lasers 289

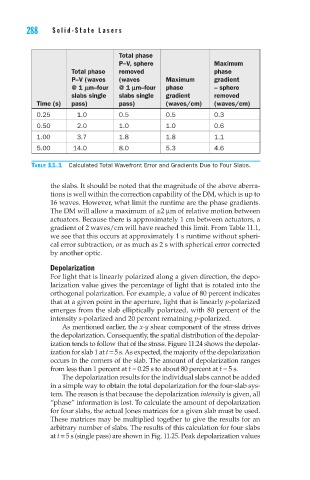
Total phase
P–V, sphere Maximum
Total phase removed phase
P–V (waves (waves Maximum gradient
@ 1 lm–four @ 1 lm–four phase – sphere
slabs single slabs single gradient removed
Time (s) pass) pass) (waves/cm) (waves/cm)
0.25 1.0 0.5 0.5 0.3
0.50 2.0 1.0 1.0 0.6
1.00 3.7 1.8 1.8 1.1
5.00 14.0 8.0 5.3 4.6

Table 11.1 Calculated Total Wavefront Error and Gradients Due to Four Slabs.

the slabs. It should be noted that the magnitude of the above aberra-
tions is well within the correction capability of the DM, which is up to
16 waves. However, what limit the runtime are the phase gradients.
The DM will allow a maximum of ±2 mm of relative motion between
actuators. Because there is approximately 1 cm between actuators, a
gradient of 2 waves/cm will have reached this limit. From Table 11.1,
we see that this occurs at approximately 1 s runtime without spheri-
cal error subtraction, or as much as 2 s with spherical error corrected
by another optic.

Depolarization
For light that is linearly polarized along a given direction, the depo-
larization value gives the percentage of light that is rotated into the
orthogonal polarization. For example, a value of 80 percent indicates
that at a given point in the aperture, light that is linearly p-polarized
emerges from the slab elliptically polarized, with 80 percent of the
intensity s-polarized and 20 percent remaining p-polarized.
As mentioned earlier, the x-y shear component of the stress drives
the depolarization. Consequently, the spatial distribution of the depolar-
ization tends to follow that of the stress. Figure 11.24 shows the depolar-
ization for slab 1 at t = 5 s. As expected, the majority of the depolarization
occurs in the corners of the slab. The amount of depolarization ranges
from less than 1 percent at t = 0.25 s to about 80 percent at t = 5 s.
The depolarization results for the individual slabs cannot be added
in a simple way to obtain the total depolarization for the four-slab sys-
tem. The reason is that because the depolarization intensity is given, all
“phase” information is lost. To calculate the amount of depolarization
for four slabs, the actual Jones matrices for a given slab must be used.
These matrices may be multiplied together to give the results for an
arbitrary number of slabs. The results of this calculation for four slabs
at t = 5 s (single pass) are shown in Fig. 11.25. Peak depolarization values