Page 126 - Hydrogeology Principles and Practice

HYDC03 12/5/05 5:37 PM Page 109

Chemical hydrogeology 109

Table 3.10 Table of reduction reactions of importance in as pe–pH stability diagrams. Methods for the con-
groundwater. After Champ et al. (1979). struction of pe–pH diagrams are presented by Stumm
and Morgan (1981). As an example, a Fe stability
o
Reaction pe = log K
10
diagram is shown in Fig. 3.20. The equilibrium equa-
−
+
1
1
(1) /4O 2(g) + H + e = /2H O +20.75 tions required to construct this type of diagram pro-
2
−
−
+
3
6
1
1
(2) /5NO + /5H + e = /10N 2(g) + /5H O +21.05 vide boundary conditions towards which a redox
2
3
+
−
2+
1
1
(3) /2MnO 2(s) + 2H + e = /2Mn + H O +20.8
2
+
−
−
+
1
5
1
3
(4) /8NO + /4H + e = /8NH + /8H O +14.9
2
3
4
+
−
2+
(5) Fe(OH) 3(s) + 3H + e = Fe + 3H O +17.1
2
2−
+
−
−
1
1
9
1
(6) /8SO + /8H + e = /8HS + /2H O +4.25
4
2
−
+
1
1
1
(7) /8CO 2(g) + H + e = /8CH 4(g) + /4H O +2.87
2
−
+
4
1
1
(8) /6N 2(g) + /3H + e = /3NH 4 + +4.68
−
+
1
1
1
(9) /4CO 2(g) + H + e = /4CH O + /4H O −1.20
2
2
of decreasing oxidizing ability, such that species
o
associated with a reaction of more positive pe act as
electron acceptors or oxidizing agents in the oxidation
of species associated with reactions of significantly
o
more negative pe .
As an example of this law of mass action approach
to redox reactions, the following equilibrium constants
can be written for the two half-reactions describing
2+ 3+
the oxidation of Fe to Fe by free oxygen (eqs 3.28
and 3.29):
=
=
K 1 10 20 .75 eq. 3.37
−
Po / 14 [H + e ][ ]
2
=
K [Fe + 2 ] − = 10 13 .05 eq. 3.38
+ 3
[Fe e ][ ]
Rewriting equations 3.37 and 3.38 in logarithmic
form produces:
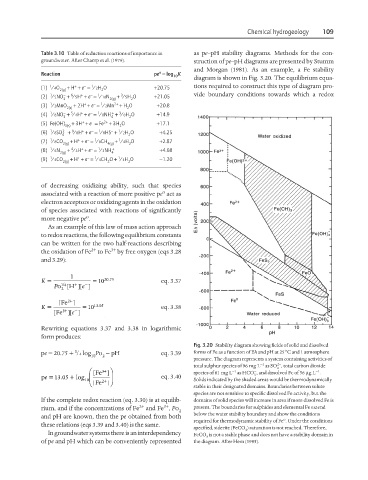
Fig. 3.20 Stability diagram showing fields of solid and dissolved
1
pe = 20.75 + /4 log Po − pH eq. 3.39 forms of Fe as a function of Eh and pH at 25°C and 1 atmosphere
10 2
pressure. The diagram represents a system containing activities of
2−
−1
total sulphur species of 96 mg L as SO , total carbon dioxide
4
[ ⎛ Fe ]⎞ species of 61 mg L as HCO , and dissolved Fe of 56 µgL .
−
+ 3
−1
−1
=
+
05
pe . log ⎜ ⎟ eq. 3.40 3
13
10 [ ⎝ Fe ]⎠ Solids indicated by the shaded areas would be thermodynamically
+ 2
stable in their designated domains. Boundaries between solute
species are not sensitive to specific dissolved Fe activity, but the
If the complete redox reaction (eq. 3.30) is at equilib- domains of solid species will increase in area if more dissolved Fe is
2+ 3+
rium, and if the concentrations of Fe and Fe , Po present. The boundaries for sulphides and elemental Fe extend
2
and pH are known, then the pe obtained from both below the water stability boundary and show the conditions
o
required for thermodynamic stability of Fe . Under the conditions
these relations (eqs 3.39 and 3.40) is the same.
specified, siderite (FeCO ) saturation is not reached. Therefore,
3
In groundwater systems there is an interdependency FeCO is not a stable phase and does not have a stability domain in
3
of pe and pH which can be conveniently represented the diagram. After Hem (1985).