Page 204 - Innovations in Intelligent Machines

196 R.W. Beard
qV a sin θ +sin θ
⎛ ⎞
g
⎜ rV a cos θ−pV a sin θ ⎟
h(x, u)= ⎜ − cos θ sin φ ⎟ .
g
⎝ ⎠
−qV a cos θ
g − cos θ cos φ
Implementation of the extended Kalman filter requires the Jacobians
q sin φ−r cos φ
∂f q cos φ tan θ − r sin φ tan θ cos 2 θ
=
∂x −q sin φ − r cos φ 0
⎛ qV a ⎞
0 cos θ +cos θ
g
∂h ⎜ rV a pV a ⎟
⎟
⎜ − cos φ cos θ − g sin θ − g cos θ +sin φ sin θ ⎟ .
∂x = ⎜ ⎠
⎝
sin φ cos θ qV a +cos φ sin θ
g
The state estimation algorithm is given by Algorithm 2.
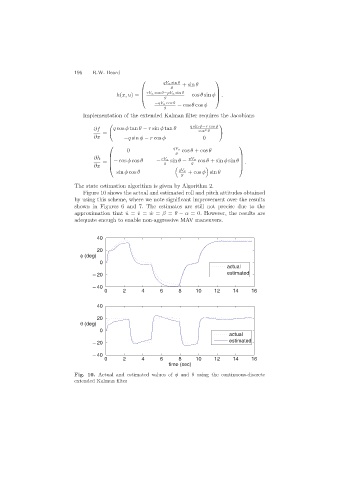
Figure 10 shows the actual and estimated roll and pitch attitudes obtained
by using this scheme, where we note significant improvement over the results
shown in Figures 6 and 7. The estimates are still not precise due to the
approximation that ˙u =˙v =˙w = β = θ − α = 0. However, the results are
adequate enough to enable non-aggressive MAV maneuvers.

40
20
φ (deg)
0
actual
- 20 estimated
- 40
0 2 4 6 8 10 12 14 16

40
20
θ (deg)
0
actual

- 20 estimated

- 40
0 2 4 6 8 10 12 14 16
time (sec)
Fig. 10. Actual and estimated values of φ and θ using the continuous-discrete
extended Kalman filter