Page 188 - Inorganic Mass Spectrometry - Fundamentals and Applications

Secondary Ion Muss Spectrometry 1 75

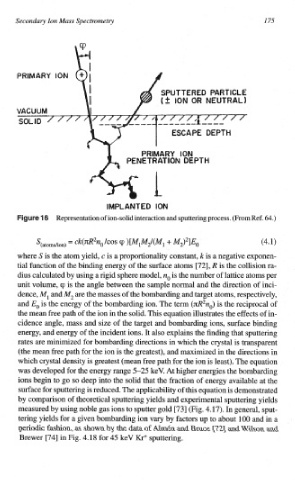
Representation of ion-solid interaction and sputtering process. (From Ref. 64.)

ck(~R2no/cos
Q,
S~~~o~~,io~~ )li"M2/(" 3- M2>21q) (4.1)
=
where S is the atom yield, c is a proportionality constant, k is a negative exponen-
tial function of the binding energy of the surface atoms [72], R is the collision ra-
no is the number of lattice atoms per
dius calculated by using a rigid sphere model,
unit volume, Q, is the angle between the sample normal and the direction of inci-
dence, M, and M2 are the masses of the bombarding and target atoms, respectively,
and Eo is the energy of the bomb~ding ion. The term (~R2n~) is the reciprocal of
the mean free path of the ion in the solid. This equation illustrates the effects of in-
cidence angle, mass and size of the target and bombarding ions, surface binding
energy, and energy of the incident ions. It also explains the finding that sputtering
rates are minimized for bombarding directions in which the crystal is transparent
(the mean free path for the ion is the greatest), and maximized in the directions in
which crystal density is greatest (mean free path for the ion is least). The equation
was developed for the energy range 5-25 keV. At higher energies the bombarding
ions begin to go so deep into the solid that the fraction of energy available at the
surface for sputtering is reduced. The applicability of this equation is demonstrated
by comparison of theoretical sputtering yields and experimental sputtering yields
measured by using noble gas ions to sputter gold 1731 (Fig. 4.17). In general, sput-
tering yields for a given bombarding ion vary by factors up to about 100 and in a
periodic fashion, as shown by the data of Almkn and Bruce C721 and Wilson and
Brewer 1741 in Fig. 4.18 for 45 keV Q+ sputtering.