Page 162 - Intermediate Statistics for Dummies

12_045206 ch07.qxd 2/1/07 9:54 AM Page 141
Residual Plots for Quiz score
Normal Probability Plot of the Residuals
Residuals Versus the Fitted Values
Standardized Residual
99
2
90
1
Percent
50
0
−1
10
−2
1
7.5
10.0
5.0
0.0
2.5
−1
−2
1
2
0
Fitted Value
Standardized Residual
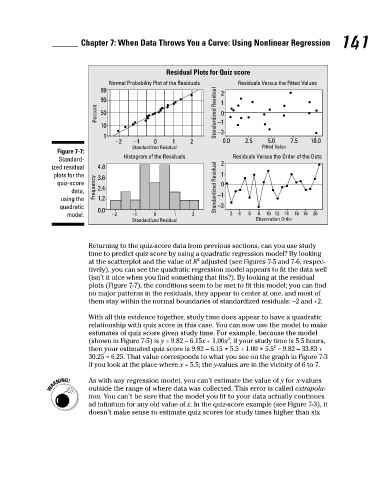
Figure 7-7:
Residuals Versus the Order of the Data
Histogram of the Residuals
Standard-
2
Standardized Residual
4.8
ized residual
1
plots for the
Frequency
3.6
quiz-score
0
2.4
data,
−1
1.2
using the
−2
quadratic Chapter 7: When Data Throws You a Curve: Using Nonlinear Regression 141
0.0
model. −2 −1 0 1 2 2 4 6 8 10 12 14 16 18 20
Standardized Residual Observation Order
Returning to the quiz-score data from previous sections, can you use study
time to predict quiz score by using a quadratic regression model? By looking
2
at the scatterplot and the value of R adjusted (see Figures 7-5 and 7-6, respec-
tively), you can see the quadratic regression model appears to fit the data well
(isn’t it nice when you find something that fits?). By looking at the residual
plots (Figure 7-7), the conditions seem to be met to fit this model; you can find
no major patterns in the residuals, they appear to center at one, and most of
them stay within the normal boundaries of standardized residuals: –2 and +2.
With all this evidence together, study time does appear to have a quadratic
relationship with quiz score in this case. You can now use the model to make
estimates of quiz score given study time. For example, because the model
2
(shown in Figure 7-5) is y = 9.82 – 6.15x + 1.00x , if your study time is 5.5 hours,
2
then your estimated quiz score is 9.82 – 6.15 5.5 + 1.00 5.5 = 9.82 – 33.83 +
*
*
30.25 = 6.25. That value corresponds to what you see on the graph in Figure 7-3
if you look at the place where x = 5.5; the y-values are in the vicinity of 6 to 7.
As with any regression model, you can’t estimate the value of y for x-values
outside the range of where data was collected. This error is called extrapola-
tion. You can’t be sure that the model you fit to your data actually continues
ad infinitum for any old value of x. In the quiz-score example (see Figure 7-3), it
doesn’t make sense to estimate quiz scores for study times higher than six