Page 25 -

3.5
∆t =1/20
3
2.5
2.5
2
0.5
0.5
1.5
1
3.5 0 ∆t =1/10 1 1.5 3.5 3 2 0 1.4 Cauchy Problems 11
3.5
∆t =1/40 ∆t =1/80
3 3
2.5 2.5
2 2
0 0.5 1 1.5 0 0.5 1 1.5
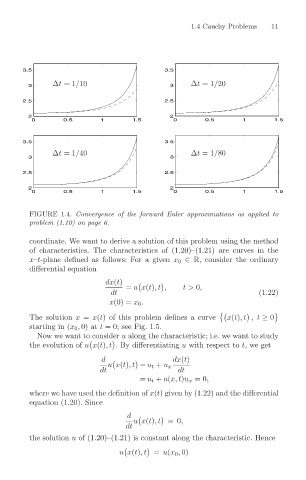
FIGURE 1.4. Convergence of the forward Euler approximations as applied to
problem (1.10) on page 6.
coordinate. We want to derive a solution of this problem using the method
of characteristics. The characteristics of (1.20)–(1.21) are curves in the
x–t-plane defined as follows: For a given x 0 ∈ R, consider the ordinary
differential equation
dx(t)
= a x(t),t , t > 0,
dt (1.22)
x(0) = x 0 .

The solution x = x(t) of this problem defines a curve x(t),t ,t ≥ 0
starting in (x 0 , 0) at t = 0; see Fig. 1.5.
Now we want to consider u along the characteristic; i.e. we want to study

the evolution of u x(t),t . By differentiating u with respect to t,weget
dx(t)
d
u x(t),t = u t + u x
dt dt
= u t + a(x, t)u x =0,
where we have used the definition of x(t) given by (1.22) and the differential
equation (1.20). Since

d
u x(t),t =0,
dt
the solution u of (1.20)–(1.21) is constant along the characteristic. Hence

u x(t),t = u(x 0 , 0)