Page 202 - Introduction to Autonomous Mobile Robots

Mobile Robot Localization

X I 187

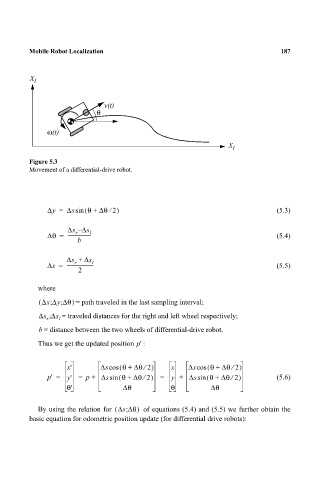
v(t)
θ

ω(t)
X I

Figure 5.3
Movement of a differential-drive robot.

⁄
∆y = ∆ssin ( θ + ∆θ 2) (5.3)
∆s ∆– s l
r
∆θ = ------------------- (5.4)
b
∆s + ∆s l
r
∆s = ---------------------- (5.5)
2
where
( ∆x ∆y ∆θ;; ) = path traveled in the last sampling interval;

∆s ∆s; l = traveled distances for the right and left wheel respectively;
r
b = distance between the two wheels of differential-drive robot.
Thus we get the updated position :
p'

⁄
⁄
x' ∆scos ( θ + ∆θ 2) x ∆scos ( θ + ∆θ 2)
⁄
⁄
p' = y' = p + ∆ssin ( θ + ∆θ 2) = y + ∆ssin ( θ + ∆θ 2) (5.6)
θ' ∆θ θ ∆θ
By using the relation for ∆s ∆θ;( ) of equations (5.4) and (5.5) we further obtain the
basic equation for odometric position update (for differential drive robots):