Page 256 - Introduction to Autonomous Mobile Robots

241
Mobile Robot Localization
3. Measurement prediction. Based on the stored map and the predicted robot position
p ˆ k k) , the measurement predictions of expected features z ti are generated (figure 5.31).
(
,
To reduce the required calculation power, there is often an additional step that first selects
the possible features, in this case lines, from the whole set of features in the map. These
lines are stored in the map and specified in the world coordinate system W{} . Therefore
they need to be transformed to the robot frame R{} :

W R
W α ti R α ti
,
,
z = → z = (5.63)
,
,
ti ti
r r
,
,
ti ti
According to figure (5.31), the transformation is given by
R α
,
(
(
(
z ˆ k + 1) = ti = h z , p ˆ k + 1 k))
,
ti
i
i
r ti
,
ˆ
(
W α – W θ k + 1 k)
(
,
z ˆ k + 1) = ti (5.64)
i
(
(
W W W W W
r – ( x ˆ k + 1 k) cos ( α ) + y ˆ k + 1 k) sin ( α ))
,
,
,
ti ti ti
and its Jacobian h∇ i by
(
θ k + 1)
(
xk + 1)
R
α (
(
i pk + 1) = yk + 1)
(
θ k + 1))
{} R
R
r
i
y W
r
i
W
α
i
{} x
W
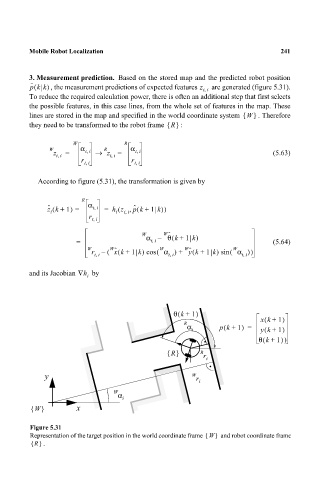
Figure 5.31
Representation of the target position in the world coordinate frame W{} and robot coordinate frame
{} .
R