Page 302 - Introduction to Autonomous Mobile Robots

Planning and Navigation

6.2.2.11 Other approaches 287
The approaches described above are some of the most popularly referenced obstacle avoid-
ance systems. There are, however, a great many additional obstacle avoidance techniques
in the mobile robotics community. For example Tzafestas and Tzafestas [148] provide an
overview of fuzzy and neurofuzzy approaches to obstacle avoidance. Inspired by nature,
Chen and Quinn [56] present a biological approach in which they replicate the neural net-
work of a cockroach. The network is then applied to a model of a four-wheeled vehicle.
The Liapunov functions form a well known theory that can be used to prove stability for
nonlinear systems. In the paper of Vanualailai, Nakagiri, and Ha [153] the Liapunov func-
tions are used to implement a control strategy for two-point masses moving in a known
environment. All obstacles are defined as antitargets with an exact position and a circular
shape. The antitargets are then used when building up the control laws for the system. How-
ever, this complex mathematical model has not been tested on a real-world robot to our
knowledge.

6.2.2.12 Overview
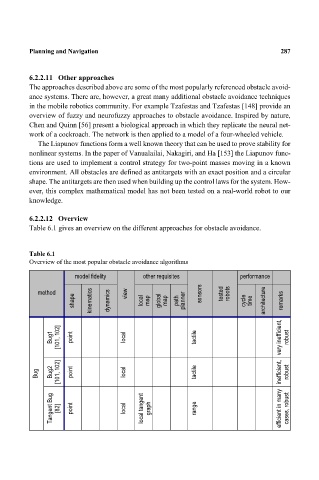
Table 6.1 gives an overview on the different approaches for obstacle avoidance.

Table 6.1
Overview of the most popular obstacle avoidance algorithms
model fidelity other requisites performance

method view sensors tested robots
shape kinematics dynamics local map global map path planner cycle time architecture remarks

Bug1 [101, 102] point local tactile very inefficient, robust

Bug Bug2 [101, 102] point local tactile inefficient, robust

Tangent Bug [82] point local local tangent graph range efficient in many cases, robust