Page 71 - Introduction to Autonomous Mobile Robots

56

Y R Chapter 3

β(t)

Robot chassis
ϕ, r
l A v
α

X
P R
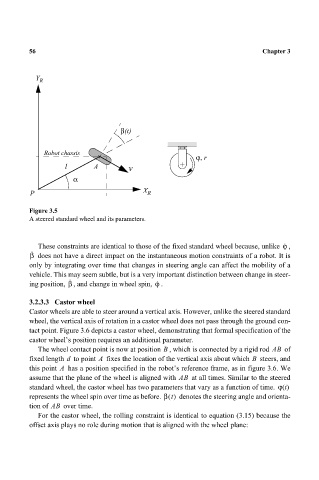
Figure 3.5
A steered standard wheel and its parameters.

ϕ
·
These constraints are identical to those of the fixed standard wheel because, unlike ,
β · does not have a direct impact on the instantaneous motion constraints of a robot. It is
only by integrating over time that changes in steering angle can affect the mobility of a
vehicle. This may seem subtle, but is a very important distinction between change in steer-
·
β
·
ϕ
ing position, , and change in wheel spin, .
3.2.3.3 Castor wheel
Castor wheels are able to steer around a vertical axis. However, unlike the steered standard
wheel, the vertical axis of rotation in a castor wheel does not pass through the ground con-
tact point. Figure 3.6 depicts a castor wheel, demonstrating that formal specification of the
castor wheel’s position requires an additional parameter.
The wheel contact point is now at position , which is connected by a rigid rod AB of
B
B
A
fixed length d to point fixes the location of the vertical axis about which steers, and
A
this point has a position specified in the robot’s reference frame, as in figure 3.6. We
assume that the plane of the wheel is aligned with AB at all times. Similar to the steered
standard wheel, the castor wheel has two parameters that vary as a function of time. ϕ t()
represents the wheel spin over time as before. β t() denotes the steering angle and orienta-
tion of AB over time.
For the castor wheel, the rolling constraint is identical to equation (3.15) because the
offset axis plays no role during motion that is aligned with the wheel plane: