Page 158 - Introduction to Computational Fluid Dynamics

P1: IWV
CB908/Date
0521853265c05
5.5 NOTION OF SMOOTHING PRESSURE CORRECTION
0.1 0 521 85326 5 May 20, 2005 12:28 137
COLLOCATED - Ru
COLLOCATED - Rv
0.01
COLLOCATED - Rm
RESIDUALS 0.001 STAGGERED - Rv
STAGGERED - Ru

STAGGERED - Rm

0.0001

1E-5
∗
41 4 1 GRIDS

1E-6
ITERATIONS
50 100 150 200 250 300 350
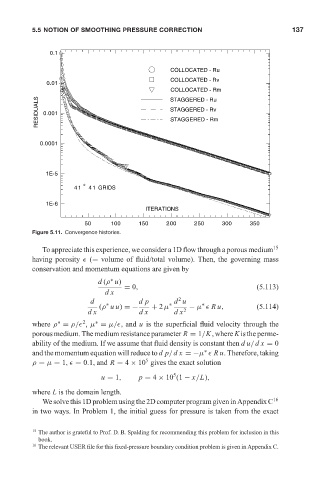
Figure 5.11. Convergence histories.

To appreciate this experience, we consider a 1D flow through a porous medium 15
having porosity (= volume of fluid/total volume). Then, the governing mass
conservation and momentum equations are given by
∗
d (ρ u)
= 0, (5.113)
dx
2
d dp d u
∗ ∗ ∗
(ρ uu) =− + 2µ − µ Ru, (5.114)
dx dx dx 2
2
where ρ = ρ/ , µ = µ/ , and u is the superficial fluid velocity through the
∗
∗
porous medium. The medium resistance parameter R = 1/K, where K is the perme-
ability of the medium. If we assume that fluid density is constant then du/dx = 0
and the momentum equation will reduce to dp/dx =−µ Ru. Therefore, taking
∗
5
ρ = µ = 1, = 0.1, and R = 4 × 10 gives the exact solution
5
u = 1, p = 4 × 10 (1 − x/L),
where L is the domain length.
Wesolvethis1Dproblemusingthe2DcomputerprogramgiveninAppendixC 16
in two ways. In Problem 1, the initial guess for pressure is taken from the exact

15 The author is grateful to Prof. D. B. Spalding for recommending this problem for inclusion in this
book.
16 The relevant USER file for this fixed-pressure boundary condition problem is given in Appendix C.